
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(2)求函数![]() 的极值点;
的极值点;
(3)设![]() ,若当
,若当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 无极值点;当
无极值点;当![]() 时,
时,![]() 的极小值点是
的极小值点是![]() ,无极大值点;(3)
,无极大值点;(3)![]() .
.
【解析】
(1)先求出函数的导函数,由切点处的导数等于切线的斜率,得到关于![]() 、
、![]() 的一个方程,再由
的一个方程,再由![]() 处的切线方程为
处的切线方程为![]() 得出切点坐标,由切点在曲线上得到关于
得出切点坐标,由切点在曲线上得到关于![]() 、
、![]() 的方程,联立关于
的方程,联立关于![]() 、
、![]() 的方程的两个方程组即可.
的方程的两个方程组即可.
(2)先求出导函数,判断函数的单调性,然后根据极值的定义求出即可.
(3)化简![]() 得
得![]() 由不等式
由不等式![]() 恒成立,转化为
恒成立,转化为![]() 恒成立,只需
恒成立,只需![]() ,通过讨论
,通过讨论![]() 的范围,求出
的范围,求出![]() 即可.
即可.
(1)由![]() 得
得![]()
![]()
由已知可得: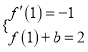 即
即![]()
![]()
(2)![]()
![]()
所以:当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上为增函数,无极值点
上为增函数,无极值点
当![]() ,即
,即![]() 时,
时,
则有:当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 在
在![]() 为减函数,在
为减函数,在![]() 上为增函数,
上为增函数,
所以,![]() 是
是![]() 极小值点,无极大值点;
极小值点,无极大值点;
综上可知:当![]() 时,函数
时,函数![]() 无极值点,
无极值点,
当![]() 时,函数
时,函数![]() 的极小值点是
的极小值点是![]() ,无极大值点
,无极大值点
(3)![]()
由题意知:当![]() 时,
时,![]() 恒成立
恒成立
又不等式![]() 等价于:
等价于:![]() ,即
,即![]()
即![]() ①
①
①式等价于![]()
由![]() 知,
知,![]()
令![]() ,则原不等式即为:
,则原不等式即为:![]()
又![]() 在
在![]() 上为增函数
上为增函数
所以,原不等式等价于:![]() , ②
, ②
又②式等价于![]() ,即:
,即:![]()
设![]() ,
,![]()
![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,
上为减函数,
又![]()
![]() 当
当![]() 时,
时,![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数
上为减函数
![]()
要使原不等式恒成立,须使![]() ,
,
当![]() 时,则
时,则![]() 在
在![]() 上为减函数,
上为减函数,![]()
要使原不等式恒成立,须使![]() ,
,
![]() 时,原不等式恒成立
时,原不等式恒成立
综上可知:![]() 的取值范围是
的取值范围是![]() ,
,![]() 的最小值为
的最小值为![]()


科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上一动点,点
上一动点,点![]() 是
是![]() 的中点.
的中点.
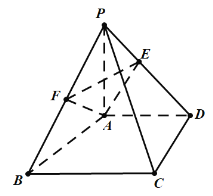
(1)求证:![]() ;
;
(2)若![]() ,问是否存在点E,使得二面角
,问是否存在点E,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出点E的位置;若不存在,请说明理由.
?若存在,求出点E的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方体![]() ,
,![]() ,
,![]() ,
,![]() ,已知P是矩形
,已知P是矩形![]() 内一动点,
内一动点,![]() 与平面
与平面![]() 所成角为
所成角为![]() ,设P点形成的轨迹长度为
,设P点形成的轨迹长度为![]() ,则
,则![]() _________;当
_________;当![]() 的长度最短时,三棱锥
的长度最短时,三棱锥![]() 的外接球的表面积为_____________.
的外接球的表面积为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,点D,E分别是线段BC,
,点D,E分别是线段BC,![]() 上的动点(不含端点),且
上的动点(不含端点),且![]() .则下列说法正确的是( )
.则下列说法正确的是( )
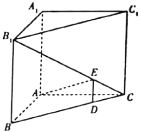
A.![]() 平面
平面![]()
B.该三棱柱的外接球的表面积为![]()
C.异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]()
D.二面角![]() 的余弦值为
的余弦值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】线段AB为圆O的直径,点E,F在圆O上,AB//EF,矩形ABCD所在平面和圆O所在平面垂直,且![]() .则( )
.则( )
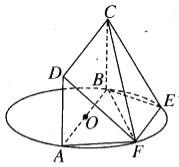
A.DF//平面BCE
B.异面直线BF与DC所成的角为30°
C.△EFC为直角三角形
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第41届世界博览会于2010年5月1日至10月31日,在中国上海举行,气势磅礴的中国馆——“东方之冠”令人印象深刻,该馆以“东方之冠,鼎盛中华,天下粮仓,富庶百姓”为设计理念,代表中国文化的精神与气质.其形如冠盖,层叠出挑,制似斗拱.它有四根高33.3米的方柱,托起斗状的主体建筑,总高度为60.3米,上方的“斗冠”类似一个倒置的正四棱台,上底面边长是139.4米,下底面边长是69.9米,则“斗冠”的侧面与上底面的夹角约为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com