
����Ŀ��ij������ֱ���ֲ�˼�������ˮ����Ϊ���о�������ˮ���IJ���������˼ס�������ˮ���Ĺ����1000�꣮��ͳ�ƣ��õ�ÿ������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��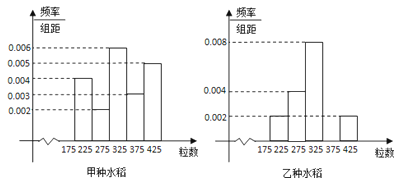
����������ˮ���������������[325��375��֮���Ƶ�ʣ�����Ƶ�ʷֲ�ֱ��ͼ���룻
�����Ը���Ƶ�ʷֲ�ֱ��ͼ���Ƽ���ˮ��������������λ����ƽ��������ȷ��0.1����
������Ƶ�ʷֲ�ֱ��ͼ�������ٴ�������Լ�������ˮ������������������ۣ�
���𰸡��⣺��������ˮ���������������[325��375��֮���Ƶ��Ϊ1��50����0.002+0.004+0.008+0.002��=0.2��
Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��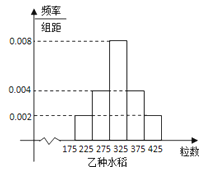
��������λ������ֵΪx������ 50����0.004+0.002��+��x��275����0.006=0.5�����x=308.3
��ֱ��ͼ��ƽ�����Ĺ���ֵΪ50��0.004��200+50��0.002��250+50��0.006��300+50��0.003��350+50��0.005��400=307.5��
����λ����ƽ�����Ĺ���ֵ�ֱ�Ϊ308.3��307.5��
���������ҵ��ȹ�������ƽ��ֵ�Ĺ���ֵΪ300��307.5
�ʿɵó����ۣ��ҵ��ȹ����������������ڼ���ˮ�����ִ�Ƶ�ʷֲ�ֱ��ͼ�ɿ����ҵ��ȹ��������ȼ���ˮ��Ҫ���룮
����������I������Ƶ�ʷֲ�ֱ��ͼ��С���ε������Ϊ1����������[325��375���ڵ�Ƶ�ʣ��������Ϊ50�����С���εĸߣ�
��II��������λ������������С���ε��������ȣ���ô���ʼ�����Ϊ0.5��С���εױߺ�����ֵ����Ϊ��λ�����������С���εĵױ��м�ֵ���������֮�ͣ���Ϊ���ݵ�ƽ������
��III�����ݼס�������ˮ��������ƽ������С��Ƶ�ʷֲ����˵����
�����㾫����������Ҫ��������������������������������������������֪ʶ�㣬��Ҫ������������������ʱ����������ķ����ȽϺ�������ô�������Է�ӳ�������Ϣ�����������õ�����Ϣ����ƫ�����������У�����ƫ���Dz��ɱ���IJ�����ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017����ʦ����ѧ������ѧ��ģ����֪����![]() ����Ȼ�����ĵ���).
����Ȼ�����ĵ���).
(1)����![]() �ĵ�������;
�ĵ�������;
(2)��![]() ,��
,��![]() ʱ,����
ʱ,����![]() �����ֵ;
�����ֵ;
(3)��![]() ��
��![]() ,��֤:
,��֤: ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֲ�Ʒ�Ĺ���֧��x�����۶�y����λ����Ԫ��֮�������¶�Ӧ���ݣ�
P��k2��k�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
������ɢ��ͼ��
������ع�ֱ�߷��̣�
������Ԥ�����֧��Ϊ10��Ԫʱ�����۶���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��2008�걱�����˻��ϣ���λ��ίΪij������Ŀ����ķ����ľ�Ҷͳ��ͼ��ȥ��һ����߷ֺ�һ����ͷֺ���ʣ���ݵ�ƽ����Ϊ ������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѡ��4��4������ϵ��������̣���֪����![]() �ļ����귽����
�ļ����귽����![]() ,����
,����![]() ����ƽ�Ʊ任
����ƽ�Ʊ任![]() �õ�����
�õ�����![]() ���Լ���Ϊԭ��,����Ϊ
���Լ���Ϊԭ��,����Ϊ![]() ����������ƽ��ֱ������ϵ,ֱ��l�IJ���������
����������ƽ��ֱ������ϵ,ֱ��l�IJ���������![]() (
(![]() ����).
����).
(1)������![]() ��
�� ![]() ��ֱ�����귽��;
��ֱ�����귽��;
(2)��ֱ��l������![]() ����
����![]() ��
��![]() ����,��
����,��![]() ��ֱ������Ϊ(2,1),��
��ֱ������Ϊ(2,1),��![]() ,��ֱ��l����ͨ����.
,��ֱ��l����ͨ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() .
.
����֤���� ![]() ��ֱ��
��ֱ��![]() ����������
����������![]() �����ߣ�
�����ߣ�
������![]() ��ʹ
��ʹ![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֲ�Ʒ��������������ָ��ֵ����������������ָ��ֵ���ֵȼ����±���
����ָ��ֵ |
|
|
|
�ȼ� | ����Ʒ | ����Ʒ | һ��Ʒ |
��ij��ҵ���������ֲ�Ʒ�г�ȡ200��������õ����µ�Ƶ�ʷֲ�ֱ��ͼ��
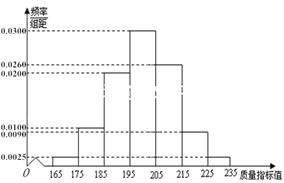
���������ϳ����������ݣ��ܷ���Ϊ����ҵ���������ֲ�Ʒ���ϡ�һ������Ʒ����Ҫռȫ����Ʒ92%���Ĺ涨��
�����������У�����Ʒ�ȼ��÷ֲ�����ķ�����ȡ8�����ٴ���8����Ʒ�������ȡ4�������ȡ��4����Ʒ�У�һ����������Ʒ���еĸ��ʣ�
������ҵΪ��߲�Ʒ��������չ�ˡ����������¡��������ٳ�����⣬��Ʒ����ָ��ֵ![]() ��������
��������![]() �������������¡���������ָ��ֵ�ľ�ֵ�Ȼǰ��Լ�����˶��٣�
�������������¡���������ָ��ֵ�ľ�ֵ�Ȼǰ��Լ�����˶��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�о���ѧϰС��Ը�У����ѧ������������е��飬�ڸ�����ȫ��![]() ��ѧ���������ȡ��
��ѧ���������ȡ��![]() ��ѧ�������������õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
��ѧ�������������õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
�꼶���� �Ƿ���� |
|
|
���� |
|
|
������ |
|
|
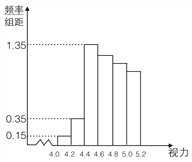
��1����ֱ��ͼ�к������Ƶ���ɵȲ����У��Թ���ȫ�꼶������![]() ���µ�������
���µ�������
��2��ѧϰС���Ա���֣�ѧϰ�ɼ�ͻ����ѧ�������ӵıȽ϶࣬Ϊ���о�ѧ����������ѧϰ�ɼ��Ƿ��й�ϵ�����꼶������![]() ����
����![]() ����ѧ�������˵��飬�õ��ұ������ݣ����ݱ��е����ݣ��ܷ��ڷ����ĸ��ʲ�����
����ѧ�������˵��飬�õ��ұ������ݣ����ݱ��е����ݣ��ܷ��ڷ����ĸ��ʲ�����![]() ��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ?
��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ?
��3���ڣ����е����![]() ��ѧ���У����շֲ�����ڲ����ӵ�ѧ���г�ȡ��
��ѧ���У����շֲ�����ڲ����ӵ�ѧ���г�ȡ��![]() �ˣ���һ�������������õĻ���ϰ�ߣ���������
�ˣ���һ�������������õĻ���ϰ�ߣ���������![]() ������ȡ
������ȡ![]() �ˣ���������
�ˣ���������![]() ��ѧ������Ϊ
��ѧ������Ϊ![]() ����
����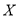 �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
|
|
|
|
|
|
|
|
|
|
| 7.879 |
![]()
���� 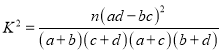
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʱ����ˬ�ڡ����ɷ�Բͼע���жԹ��ɶ�����֤�������ִ���ѧ����Ϊ��ͼ��ʾ�����ǽ̲������ø�ͼ��Ϊ���� �����ļ��ν��ͣ� 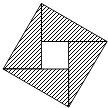
A.���a��b��b��c����ôa��c
B.���a��b��0����ôa2��b2
C.������ʵ��a��b����a2+b2��2ab�����ҽ���a=bʱ�Ⱥų���
D.���a��b��c��0��ôac��bc
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com