[题目]意大利著名数学家斐波那契在研究兔子的繁殖问题时.发现有这样的一列数:1.1.2.3.5.8.-.该数列的特点是:前两个数均为1.从第三个数起.每一个数都等于它前面两个数的和．人们把这样的一列数组成的数列{an}称为斐波那契数列.则 ﹣ =( )A.0B.﹣1C.1D.2 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】意大利著名数学家斐波那契在研究兔子的繁殖问题时，发现有这样的一列数：1，1，2，3，5，8，…，该数列的特点是：前两个数均为1，从第三个数起，每一个数都等于它前面两个数的和．人们把这样的一列数组成的数列{an}称为斐波那契数列，则 ﹣ =（）
A.0
B.﹣1
C.1
D.2

【答案】A
【解析】解：a1a3﹣a22=1×2﹣1=1， a2a4﹣a32=1×3﹣22=﹣1，
a3a5﹣a42=2×5﹣32=1，
…
a8a10﹣a92=1
∴ ﹣ =（a1a3+a2a4+…a8a10）﹣（a22+a32+…+a92）=0
故选：A
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系．

练习册系列答案

中考速递河南中考系列答案

PASS教材搭档系列答案

天利38套中考总复习命题规律与必考压轴题系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】用，，，，，这六个数字．

（）能组成多少个无重复数字的四位偶数．

（）能组成多少个比大的四位数．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数的最小正周期为，且其图象的一个对称轴为，将函数图象上所有点的橫坐标缩小到原来的倍，再将图象向左平移个单位长度，得到函数的图象.

（1）求的解析式，并写出其单调递增区间；

（2）求函数在区间上的零点；

（3）对于任意的实数，记函数在区间上的最大值为，最小值为，求函数在区间上的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设f（x）=ex﹣e﹣x﹣x．
（1）求f（x）的单调区间；
（2）已知g（x）=x2f（x）+（x+1）[f（x）+（1﹣a）x]+（1﹣a）x3 ．若对所有x≥0，都有g（x）≥0成立，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图所示，在以为直径的半圆周上，有异于的六个点，直径上有异于的四个点.则：

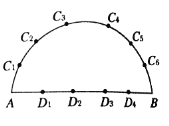
（1）以这12个点（包括）中的4个点为顶点，可作出多少个四边形？

（2）以这10个点（不包括）中的3个点为顶点，可作出多少个三角形？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列{an}的前n项和为Sn ，且满足a1=1，anan+1=2Sn ，设bn= ，若存在正整数p，q（p＜q），使得b1 ， bp ， bq成等差数列，则p+q= ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某农科所发现，一中作物的年收获量y（单位：kg）与它”相近“作物的株数x具有线性相关关系（所谓两株作物”相近“是指它们的直线距离不超过1m），并分别记录了相近作物的株数为1，2，3，5，6，7时，该作物的年收获量的相关数据如下：

X	1	2	3	5	6	7
y	60	55	53	46	45	41

（Ⅰ）求该作物的年收获量y关于它”相近“作物的株数x的线性回归方程；
（Ⅱ）农科所在如图所示的正方形地块的每个格点（指纵、横直线的交叉点）处都种了一株该作物，其中每一个小正方形的面积为1，若在所种作物中随机选取一株，求它的年收获量的分布列与数学期望．（注：年收获量以线性回归方程计算所得数据为依据）
附：对于一组数据（x1 ， y1），（x2 ， y2），…，（xn ， yn），其回归直线y=a+bx的斜率和截距的最小二乘估计分别为 = = ， = ﹣ ．