练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．根据现行国家标准GB3095-2012，PM2.5日均值在35微克/立方米以下空气质量为一级；在35～75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．
    从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本，监测值频数如茎叶图所示（十位为茎，个位为叶）：
    （I）求空气质量为超标的数据的平均数与方差；
    （II）从空气质量为二级的数据中任取2个，求这2个数据的和小于100的概率；
    （III）以这12天的PM2.5日均值来估计2012年的空气质量情况，估计2012年（366天）大约有多少天的空气质量达到一级或二级．

    分析 （I）由茎叶图求出空气质量为超标的数据，由此能求出空气质量为超标的数据的平均数与方差．
    （II）由茎叶图求出空气质量为二级的数据，由此利用列举法能求出从空气质量为二级的数据中任取2个，这2个数据和小于100的概率．
    （III）由茎叶图求出空气质量为一级或二级的数据，从而得到空气质量为一级或二级的频率，由此能求出2012年的366天中空气质量达到一级或二级的天数．

    解答 解：（I）空气质量为超标的数据有四个：77，79，84，88
    平均数为$\overline x=\frac{77+79+84+88}{4}=82$（2分）
    方差为${s^2}=\frac{1}{4}×[{（77-82）^2}+{（79-82）^2}+{（84-82）^2}+{（88-82）^2}]=18.5$（4分）
    （II）空气质量为二级的数据有五个：47，50，53，57，68
    任取两个有十种可能结果：{47，50}，{47，53}，{47，57}，{47，68}，{50，53}，
    {50，57}，{50，68}，{53，57}，{53，68}，{57，68}．
    两个数据和小于100的结果有一种：{47，50}．
    记“两个数据和小于100”为事件A，则$P（A）=\frac{1}{10}$
    即从空气质量为二级的数据中任取2个，这2个数据和小于100的概率为$\frac{1}{10}$（8分）
    （III）空气质量为一级或二级的数据共8个，
    所以空气质量为一级或二级的频率为$\frac{8}{12}=\frac{2}{3}$（10分）
    $336×\frac{2}{3}=244$，
    所以2012年的366天中空气质量达到一级或二级的天数估计为244天．（12分）

    点评 本题考查平均数、方差、概率的求法，是中档题，在历年高考中都是必考题型之一，解题时要注意茎叶图知识的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．已知函数f（x）=$\left\{\begin{array}{l}{（2a-1）x+7a-2，x＜1}\\{-a{x}^{2}-1，x≥1}\end{array}\right.$在（-∞，+∞）上单调递减，则实数a的取值范围[$\frac{1}{5}$，$\frac{1}{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

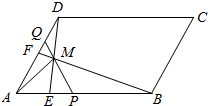    4．如图所示，在平行四边形ABCD中，$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$，$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$，BF与DE交于点M，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$．
    （1）用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{AM}$；
    （2）在线段AB上取一点P，在线段AD上取一点Q，使PQ过点M，设$\overrightarrow{AP}$=p$\overrightarrow{AB}$，$\overrightarrow{AQ}$=q$\overrightarrow{AD}$，求证：$\frac{1}{7p}$+$\frac{3}{7q}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．数列{an}的前n项和Sn，满足Sn=4an+1，则an=-$\frac{1}{3}$×$（\frac{4}{3}）^{n-1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．指出函数f（x）=$\frac{{x}^{2}+4x+5}{{x}^{2}+4x+4}$的单调区间，并比较f（-π）与f（-$\frac{\sqrt{2}}{2}$）的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设函数y=f（x）定义域为{x|x∈R且x≠1}，已知f（x+1）为奇函数，当x＜1时，f（x）=2x2-x+1，则x＞1时，f（x）的递减区间为（　　）
    A．[$\frac{5}{4}$，+∞）B．（1，$\frac{5}{4}$]C．[$\frac{7}{4}$，+∞）D．（1，$\frac{7}{4}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．从混有4件次品的20件商品中抽取3件，已知有1件是次品，求3件都是次品的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．函数f（x）具有如下性质：对每个实数x，都有f（x）+f（x-1）=x2．如果f（19）=94，那么f（94）除以1000的余数是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=ln（1+x）-ax的图象在x=1处的切线与直线x+2y-1=0平行．
    （1）求函数f（x）的单调递增区间；
    （2）若方程f（x）=$\frac{1}{4}$（m-3x）在[2，4]上有两个不相等的实数根，求实数m的取值范围．（参考数据In3≈1.0986
    ，In4≈1.3863，In5≈1.6094）

    查看答案和解析>>

    同步练习册答案