练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线C：y2=8x的焦点为F，过F作倾斜角为60°的直线l．
    （1）求直线l的方程；
    （2）求直线l被抛物线C所截得的弦长．

    【答案】
    （1）解：抛物线y2=8x的焦点F为（2，0），直线的斜率k=

    代入点斜式方程得：y= （x﹣2），即 =0


    （2）解：设直线与抛物线的交点为A（x1，y1），B（x2，y2），

    由直线与抛物线消去y得3x2﹣20x+12=0

    所以x1+x2= ，

    由抛物线的定义可得，|AB|=x1+x2+p= ，

    即直线被抛物线所截得的弦长为


    【解析】（1）求得抛物线的焦点，可得直线AB的方程；（2）由直线与抛物线消去y得3x2﹣20x+12=0，运用韦达定理和抛物线的定义，即可得到所求值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数y=f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x﹣x2 ．
    （1）求x＜0时f（x）的解析式；
    （2）问是否存在正数a，b，当x∈[a，b]时，g（x）=f（x），且g（x）的值域为[ ， ]？若存在，求出所有的a，b的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2x﹣2﹣x ， 若对任意的x∈[1，3]，不等式f（x2+tx）+f（4﹣x）＞0恒成立，则实数t的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设集合M={x|0≤x≤2}，N={y|0≤y≤2}，给出如下四个图形，其中能表示从集合M到集合N的函数关系的是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是我国2009年至2015年生活垃圾无害化处理量（单位：亿吨）的折线图.
    （Ⅰ）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；
    （Ⅱ）建立y关于t的回归方程（系数精确到0.01），预测2017年我国生活垃圾无害化处理量．
    参考数据： yi=9.32， tiyi=40.17， =0.55， ≈2.646．
    参考公式：相关系数r= =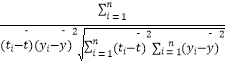
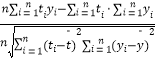
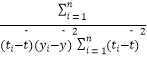    回归方程 = + t中斜率和截距的最小二乘估计公式分别为： = ， = ﹣ t．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线C：4x2﹣y2=4及直线l：y=kx﹣1
    （1）求双曲线C的渐近线方程及离心率；
    （2）直线l与双曲线C左右两支各有一个公共点，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，根据现行国家标准GB3095﹣2012，PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米～75毫克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本，监测值频数如表所示：

    PM2.5日均值
    （微克/立方米）

    [25，35]

    （35，45]

    （45，55]

    （55，65]

    （65，75]

    （75，85]

    频数

    3

    1

    1

    1

    1

    3


    （1）从这10天的PM2.5日均值监测数据中，随机抽取3天，求恰有1天空气质量达到一级的概率；
    （2）从这10天的数据中任取3天数据，记ξ表示抽到PM2.5监测数据超标的天数，求ξ的分布列；
    （3）以这10天的PM2.5日均值来估计一年的空气质量状况，则一年（按366天算）中平均有多少天的空气质量达到一级或二级．（精确到整数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】Sn表示等差数列{an}的前n项的和，且S4=S9 ， a1=﹣12
    （1）求数列的通项an及Sn；
    （2）求和Tn=|a1|+|a2|+…+|an|

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年3月29日，中国自主研制系全球最大水陆两栖飞机AG600将于2017年5月计划首飞，AG600飞机的用途很多，最主要的是森林灭火、水上救援、物资运输、海洋探测、根据灾情监测情报部门监测得知某个时间段全国有10起灾情，其中森林灭火2起，水上救援3起，物资运输5起，现从10起灾情中任意选取3起.

    （1）求三种类型灾情中各取到1个的概率；

    （2）设表示取到的森林灭火的数目，求的分布列与数学期望.

    查看答案和解析>>

    同步练习册答案