
【题目】已知函数![]() (
(![]() ),
),![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,
时,![]() 的两个极值点为
的两个极值点为![]() ,
,![]() (
(![]() ).
).
①证明:![]() ;
;
②若![]() ,
,![]() 恰为
恰为![]() 的零点,求
的零点,求![]() 的最小值.
的最小值.
【答案】(1)当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,当
,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]() .
.
【解析】
试题分析:(1)对函数求导,对参数![]() 分类讨论,利用导数的正负求得函数的单调区间;(2)①对函数求导得
分类讨论,利用导数的正负求得函数的单调区间;(2)①对函数求导得![]() ,得
,得![]() 的两根
的两根![]() ,
,![]() 即为方程
即为方程![]() 的两根;利用韦达定理得
的两根;利用韦达定理得![]() ,
,![]() ,令
,令![]() (
(![]() ),由
),由![]() ,得
,得![]() ,两边同时除以
,两边同时除以![]() ,得
,得![]() ,且
,且![]() ,求得
,求得![]() 的取值范围,从而证得结论;②由
的取值范围,从而证得结论;②由![]() ,
,![]() 为
为![]() 的零点,代入相减得
的零点,代入相减得![]() ,故
,故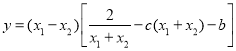
 ,令
,令![]() (
(![]() ),
),![]() ,求导后利用函数的单调性求得其最小值,从而求得所求结果.
,求导后利用函数的单调性求得其最小值,从而求得所求结果.
试题解析:(1)∵函数![]() ,∴
,∴![]() ,
,![]() ;
;
当![]() 时,由
时,由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,故
,故![]() ,即
,即![]() 在
在![]() 上单调递增;
上单调递增;
∴当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)①![]() ,则
,则![]() ,
,
∴![]() 的两根
的两根![]() ,
,![]() 即为方程
即为方程![]() 的两根;
的两根;
又∵![]() ,∴
,∴![]() ,
,![]() ,
,![]()
令![]() (
(![]() ),由
),由![]() ,得
,得![]() ,
,
因为![]() ,两边同时除以
,两边同时除以![]() ,得
,得![]() ,且
,且![]() ,
,
故![]() ,解得
,解得![]() 或
或![]() ,∴
,∴![]() ,即
,即![]() .
.
②∵![]() ,
,![]() 为
为![]() 的零点,
的零点,
∴![]() ,
,![]() ,
,
两式相减得![]() ,
,
∵![]() ,
,
∴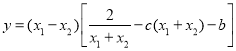
 ,
,
令![]() (
(![]() ),
),![]() ,
,
则![]() ,
,![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() ,
,
即![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3ax-1,a≠0.
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(2)对一切![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)探讨函数![]() 是否存在零点?若存在,求出函数
是否存在零点?若存在,求出函数![]() 的零点;若不存在,请说明理由.
的零点;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:
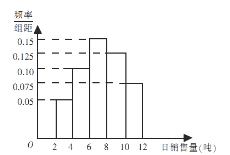
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率;
(2)用![]() 表示未来3天内日销售量不低于8吨的天数,求随机变量
表示未来3天内日销售量不低于8吨的天数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中放有的黑球和白球,其中黑球4个,白球5个.
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率.
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
(3)从盒中不放回的每次摸一球,若取到白球则停止摸球,求取到第三次时停止摸球的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东亚运动会将于2013年10月6日在天津举行.为了搞好接待工作,组委会打算学习北京奥运会招募大量志愿者的经验,在某学院招募了16名男志愿者和14名女志愿者,调查发现,男女志愿者中分别有10人和6人喜爱运动,其余人不喜欢运动.
(1)根据以上数据完成以下2×2列联表:
喜爱运动 | 不喜爱运动 | 总计 | |
男 | 10 | 16 | |
女 | 6 | 14 | |
总计 | 30 |
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有4人会外语),抽取2名负责翻译工作,那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少?
参考公式:K2=![]() ,其中
,其中
n=a+b+c+d.
参考数据:
P(K2≥k) | 0.40 | 0.25 | 0.10 | 0.010 |
k | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机抽调了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:

(1)由以上统计数据填下面![]() 列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;

(2)若对年龄在![]() 的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com