
【题目】已知曲线![]() (
(![]() 为常数).
为常数).
(i)给出下列结论:
①曲线![]() 为中心对称图形;
为中心对称图形;
②曲线![]() 为轴对称图形;
为轴对称图形;
③当![]() 时,若点
时,若点![]() 在曲线
在曲线![]() 上,则
上,则![]() 或
或![]() .
.
其中,所有正确结论的序号是_________.
(ii)当![]() 时,若曲线
时,若曲线![]() 所围成的区域的面积小于
所围成的区域的面积小于![]() ,则
,则![]() 的值可以是_________.(写出一个即可)
的值可以是_________.(写出一个即可)
【答案】①②③ ![]() 均可
均可
【解析】
(i)在曲线![]() 上任取一点
上任取一点![]() ,将点
,将点![]() 、
、![]() 、
、![]() 代入曲线
代入曲线![]() 的方程,可判断出命题①②的正误,利用反证法和不等式的性质可判断出命题③的正误;
的方程,可判断出命题①②的正误,利用反证法和不等式的性质可判断出命题③的正误;
(ii)根据![]() 时,配方得出
时,配方得出![]() ,可知此时曲线
,可知此时曲线![]() 为圆,且圆的面积为
为圆,且圆的面积为![]() ,从而得知当
,从而得知当![]() 时,曲线
时,曲线![]() 所表示的图形面积小于
所表示的图形面积小于![]() .
.
(i)在曲线![]() 上任取一点
上任取一点![]() ,则
,则![]() ,
,
将点![]() 代入曲线
代入曲线![]() 的方程可得
的方程可得![]() ,
,
同理可知,点![]() 、
、![]() 都在曲线
都在曲线![]() 上,则曲线
上,则曲线![]() 关于原点和坐标轴对称,命题①②正确.
关于原点和坐标轴对称,命题①②正确.
当![]() 时,
时,![]() ,反设
,反设![]() 且
且![]() ,
,
则![]() ,
,![]() ,所以,
,所以,![]() ,则
,则![]() ,
,
所以,![]() ,这与
,这与![]() 矛盾.
矛盾.
假设不成立,所以,![]() 或
或![]() ,命题③正确;
,命题③正确;
(ii)当![]() 时,曲线
时,曲线![]() 的方程为
的方程为![]() ,即
,即![]() ,即
,即![]() ,
,
此时,曲线![]() 表示半径为
表示半径为![]() 的圆,其面积为
的圆,其面积为![]() .
.
当![]() 时,且当
时,且当![]() 时,在圆
时,在圆![]() 上任取一点
上任取一点![]() ,则
,则![]() ,则点
,则点![]() 在曲线外,所以,曲线
在曲线外,所以,曲线![]() 的面积小于圆的面积
的面积小于圆的面积![]() .
.
故答案为:①②③;![]() 均可.
均可.


科目:高中数学 来源: 题型:
【题目】已知某超市2018年12个月的收入与支出数据的折线图如图所示:
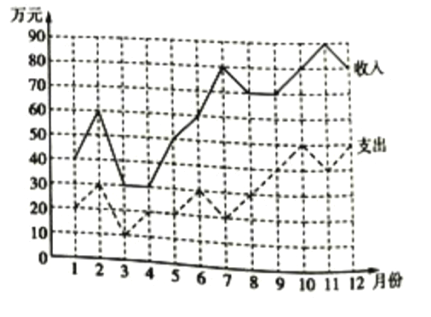
根据该折线图可知,下列说法错误的是( )
A. 该超市2018年的12个月中的7月份的收益最高
B. 该超市2018年的12个月中的4月份的收益最低
C. 该超市2018年1-6月份的总收益低于2018年7-12月份的总收益
D. 该超市2018年7-12月份的总收益比2018年1-6月份的总收益增长了90万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,
,![]() 为椭圆的左右顶点,焦点
为椭圆的左右顶点,焦点![]() 到短轴端点的距离为2,且
到短轴端点的距离为2,且![]() ,
,![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的两点,直线
的两点,直线![]() 的斜率等于直线
的斜率等于直线![]() 斜率的2倍.
斜率的2倍.
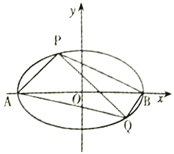
(1)求直线![]() 与直线
与直线![]() 的斜率乘积值;
的斜率乘积值;
(2)求证:直线![]() 过定点,并求出该定点;
过定点,并求出该定点;
(3)求三角形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系.已知曲线
轴正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,点
,点![]() 满足
满足![]() ,设倾斜角为
,设倾斜角为![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的参数方程;
的参数方程;
(2)直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,当
两点,当![]() 为何值时,
为何值时,![]() 最大?求出此最大值.
最大?求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的焦点为F,过F的直线
的焦点为F,过F的直线![]() 交
交![]() 于B,C两点.
于B,C两点.
(1)若![]() 垂直于轴,且线段BC的长为1,求
垂直于轴,且线段BC的长为1,求![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,求
,求![]() ;
;
(3)设抛物线上异于![]() 的点A满足
的点A满足![]() ,若
,若![]() 的重心在
的重心在![]() 轴上,求
轴上,求![]() 的重心的坐标.
的重心的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2019年女排世界杯中,中国女子排球队以11连胜的优异战绩成功夺冠,为祖国母亲七十华诞献上了一份厚礼.排球比赛采用5局3胜制,前4局比赛采用25分制,每个队只有赢得至少25分,并同时超过对方2分时,才胜1局;在决胜局(第五局)采用15分制,每个队只有赢得至少15分,并领先对方2分为胜.在每局比赛中,发球方赢得此球后可得1分,并获得下一球的发球权,否则交换发球权,并且对方得1分.现有甲乙两队进行排球比赛:
(1)若前三局比赛中甲已经赢两局,乙赢一局.接下来两队赢得每局比赛的概率均为![]() ,求甲队最后赢得整场比赛的概率;
,求甲队最后赢得整场比赛的概率;
(2)若前四局比赛中甲、乙两队已经各赢两局比赛.在决胜局(第五局)中,两队当前的得分为甲、乙各14分,且甲已获得下一发球权.若甲发球时甲赢1分的概率为![]() ,乙发球时甲赢1分的概率为
,乙发球时甲赢1分的概率为![]() ,得分者获得下一个球的发球权.设两队打了
,得分者获得下一个球的发球权.设两队打了![]() 个球后甲赢得整场比赛,求x的取值及相应的概率p(x).
个球后甲赢得整场比赛,求x的取值及相应的概率p(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A-BCD中,平面ABC丄平面ADC, AD丄AC,AD=AC, ![]() ,若此三棱锥的外接球表面积为
,若此三棱锥的外接球表面积为![]() ,则三棱锥A-BCD体积的最大值为( )
,则三棱锥A-BCD体积的最大值为( )
A.7B.12C.6D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com