
分析 (Ⅰ)由已知得$\frac{2}{{a}_{n}}=\frac{1}{{a}_{n-1}}+\frac{1}{{a}_{n+1}}$,从而推导出{$\frac{1}{{a}_{n}}$}是首项为1,公差为$\frac{1}{2}$的等差数列,由此能求出数列{an}的通项公式.
(Ⅱ)由bn=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,利用错位相减法能证明Tn<1.
解答 (本小题满分12分)
解:(Ⅰ)∵数列{an}满足:a1=1,3a2-a1=1,且$\frac{2}{{a}_{n}}$=$\frac{{a}_{n-1}+{a}_{n+1}}{{a}_{n-1}{a}_{n+1}}$(n≥2),
∴$\frac{2}{{a}_{n}}=\frac{1}{{a}_{n-1}}+\frac{1}{{a}_{n+1}}$,…(1分)
又a1=1,3a2-a1=1,
∴$\frac{1}{{a}_{1}}=1,\frac{1}{{a}_{2}}=\frac{3}{2}$,∴$\frac{1}{{a}_{2}}-\frac{1}{{a}_{1}}$=$\frac{1}{2}$,…(3分)
∴{$\frac{1}{{a}_{n}}$}是首项为1,公差为$\frac{1}{2}$的等差数列,…(5分)
∴$\frac{1}{{a}_{n}}$=1+$\frac{1}{2}(n-1)=\frac{1}{2}(n+1)$,
∴an=$\frac{2}{n+1}$.…(7分)
(Ⅱ)证明:∵数列b1=$\frac{1}{2}$,4bn=an-1an,
∴bn=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,…(9分)
∴Tn=b1+b2+…+bn=(1-$\frac{1}{2}$)+($\frac{1}{2}-\frac{1}{3}$)+…+($\frac{1}{n}-\frac{1}{n+1}$)=$1-\frac{1}{n+1}$<1.
故Tn<1.…(12分)
点评 本题考查数列的通项公式的求法,考查数列的前n项和小于1的证明,是中档题,解题时要认真审题,注意裂项求和法的合理运用.


科目:高中数学 来源: 题型:选择题
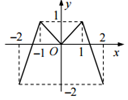 如图,定义在[-2,2]的偶函数f(x)的图象如图所示,函数g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零点个数为( )
如图,定义在[-2,2]的偶函数f(x)的图象如图所示,函数g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零点个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
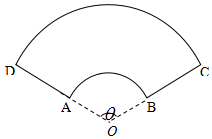 某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).
某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
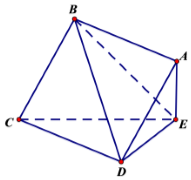 如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.
如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{63}$ | B. | $\frac{50}{63}$ | C. | $\frac{43}{63}$ | D. | $\frac{11}{63}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com