
分析 (1)a=1时,求出集合B,然后进行补集、交集的运算即可;
(2)讨论a:分a=0,a<0,和a>0三种情况,对于每种情况求出集合B,根据A⊆B求出a的范围,再求并集即可得出a的取值范围.
解答 解:(1)当a=1时,$B=\{x|2x-5>0\}=\left\{{x|x>\frac{5}{2}}\right\}$,${C_R}B=\left\{{x|x≤\frac{5}{2}}\right\}$,∁RA={x|x<1};
∴(∁UA)∩(∁UB)={x|x<1};
(2)①当a=0时,B=∅,不满足A⊆B;
②当a<0时,B={x|$x<\frac{5}{2a}$},不满足A⊆B;
③当a>0时,$B=\{x|2ax-5>0\}=\left\{{x|x>\frac{5}{2a}}\right\}$,A⊆B则:
$\frac{5}{2a}<1$,$a>\frac{5}{2}$;
∴a的取值范围为($\frac{5}{2}$,+∞).
点评 考查描述法表示集合,交集、补集的运算,以及子集的概念,可借助数轴.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
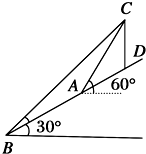 如图,要在山坡上A、B两处测量与地面垂直的铁塔CD的高,由A、B两处测得塔顶C的仰角分别为60°和45°,AB长为48m,斜坡与水平面成30°角,则铁塔CD的高为16$\sqrt{3}$m.
如图,要在山坡上A、B两处测量与地面垂直的铁塔CD的高,由A、B两处测得塔顶C的仰角分别为60°和45°,AB长为48m,斜坡与水平面成30°角,则铁塔CD的高为16$\sqrt{3}$m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
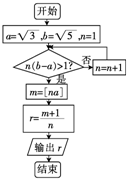
| A. | $\frac{7}{3}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com