
【题目】已知函数f(x)=asin2x﹣2cos2x+1(a∈R)的图象经过点(﹣![]() ,1)
,1)
(1)求a;
(2)若在区间[0,m]上存在唯一实数x0,使得f(x0)=2,求实数m的取值范围.
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
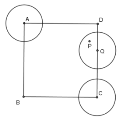
【题目】如图,边长为4的正方形![]() 中,半径为1的动圆Q的圆心Q在边CD和DA上移动(包含端点A,C,D),P是圆Q上及其内部的动点,设,
中,半径为1的动圆Q的圆心Q在边CD和DA上移动(包含端点A,C,D),P是圆Q上及其内部的动点,设,![]() 则
则![]() 的取值范围是_____________.
的取值范围是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题不正确的是( )
A.研究两个变量相关关系时,相关系数r为负数,说明两个变量线性负相关
B.研究两个变量相关关系时,相关指数R2越大,说明回归方程拟合效果越好.
C.命题“x∈R,cosx≤1”的否定命题为“x0∈R,cosx0>1”
D.实数a,b,a>b成立的一个充分不必要条件是a3>b3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设![]() :实数x满足|x﹣m|<2,设
:实数x满足|x﹣m|<2,设![]() :实数x满足
:实数x满足![]() >1;若¬p是¬q的必要不充分条件,求实数m的取值范围
>1;若¬p是¬q的必要不充分条件,求实数m的取值范围
(2)已知p:函数f(x)=ln(x2﹣ax+3)的定义城为R,已知q:已知![]() 且
且![]() ,指数函数g(x)=(a﹣1)x在实数域内为减函数;若¬p∨q为假命题,求实数a的取值范围.
,指数函数g(x)=(a﹣1)x在实数域内为减函数;若¬p∨q为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 关于直线
关于直线![]() 对称且过点
对称且过点![]() 和
和![]() ,直线
,直线![]() 过定点
过定点![]() .
.
(1)证明:直线![]() 与圆
与圆![]() 相交;
相交;
(2)记直线![]() 与圆
与圆![]() 的两个交点为
的两个交点为![]() ,
,![]() .
.
①若弦长![]() ,求直线方程;
,求直线方程;
②求![]() 面积的最大值及
面积的最大值及![]() 面积的最大时的直线方程.
面积的最大时的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
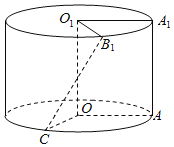
【题目】边长为1的正方形![]() (及其内部)绕的
(及其内部)绕的![]() 旋转一周形成圆柱,如图,
旋转一周形成圆柱,如图,![]() 长为
长为![]() ,
,![]() 长为
长为![]() ,其中
,其中![]() 与
与![]() 在平面
在平面![]() 的同侧.
的同侧.
(1)求二面角![]() 的大小;(结果用反三角函数值表示)
的大小;(结果用反三角函数值表示)
(2)用一平行于![]() 的平面去截这个圆柱,若该截面把圆柱侧面积分成
的平面去截这个圆柱,若该截面把圆柱侧面积分成![]() 两部分,求
两部分,求![]() 与该截面的距离;
与该截面的距离;
(3)求线段![]() ,
,![]() 绕着
绕着![]() 旋转
旋转![]() 所形成的几何体的表面积.
所形成的几何体的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com