
【题目】已知圆C的方程为:x2+y2﹣2x﹣4y+m=0.
(1)求m的取值范围;
(2)若圆C与直线3x+4y﹣6=0交于M、N两点,且|MN|=2 ![]() ,求m的值;
,求m的值;
(3)设直线x﹣y﹣1=0与圆C交于A、B两点,是否存在实数m,使得以AB为直径的圆过原点,若存在,求出实数m的值;若不存在,请说明理由.
【答案】
(1)解:∵x2+y2﹣2x﹣4y+m=0,
由D2+E2﹣4F=4+16﹣4m=20﹣4m>0,得m<5,
∴当m<5时,曲线C表示圆
(2)解:∵x2+y2﹣2x﹣4y+m=0,
∴(x﹣1)2+(y﹣2)2=5﹣m,
∴圆心C(1,2),半径r= ![]() ,
,
∵圆心C(1,2)到直线3x+4y﹣6=0的距离d= ![]() =1,
=1,
又|MN|=2 ![]() ,由r2=d2+3,即5﹣m=1+3,
,由r2=d2+3,即5﹣m=1+3,
解得m=1
(3)解:假设存在实数m使得以AB为直径的圆过原点,则OA⊥OB,
设A(x1,y1),B(x2,y2),则x1x2+y1y2=0,
由 ![]() ,
,
得2x2﹣8x+5+m=0,
∴△=64﹣8(m+5)=24﹣8m>0,即m<3,又由(1)知m<5,
故m<3,x1+x2=4,x1x2= ![]() ,
,
∴y1y2=(x1﹣1)(x2﹣1)=x1x2﹣(x1+x2)+1= ![]() ﹣4+1=
﹣4+1= ![]() ,
,
∴x1x2+y1y2= ![]() +
+ ![]() =m+2=0,
=m+2=0,
∴m=﹣2<3,
故存在实数m使得以AB为直径的圆过原点,m=﹣2
【解析】(1)由D2+E2﹣4F=4+16﹣4m=20﹣4m>0,由求出当m<5时,曲线C表示圆;(2)由已知条件推导出圆心C(1,2),半径r= ![]() ,由此利用点到直线的距离公式及弦长公式,结合已知条件能求出m=1;(3)假设存在实数m使得以AB为直径的圆过原点,则OA⊥OB,设A(x1 , y1),B(x2 , y2),则x1x2+y1y2=0,由
,由此利用点到直线的距离公式及弦长公式,结合已知条件能求出m=1;(3)假设存在实数m使得以AB为直径的圆过原点,则OA⊥OB,设A(x1 , y1),B(x2 , y2),则x1x2+y1y2=0,由 ![]() ,得2x2﹣8x+5+m=0,由此能求出存在实数m使得以AB为直径的圆过原点.
,得2x2﹣8x+5+m=0,由此能求出存在实数m使得以AB为直径的圆过原点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知an=log(n+1)(n+2)(n∈N*).我们把使乘积a1a2a3…an为整数的数n叫做“优数”,则在区间(1,2004)内的所有优数的和为( )
A.1024
B.2003
C.2026
D.2048
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别是等比数列{bn}的第2项、第3项、第4项.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对n∈N*均有 ![]() =an+1成立,求c1+c2+c3+…+c2016 .
=an+1成立,求c1+c2+c3+…+c2016 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数 ![]() .
.
(1)若f(x)是奇函数,求m的值;
(2)当m=1时,求函数f(x)在(﹣∞,0)上的值域,并判断函数f(x)在(﹣∞,0)上是否为有界函数,请说明理由;
(3)若函数f(x)在[0,1]上是以3为上界的函数,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两组数据的茎叶如图所示,若它们的平均数相同,则下列关于甲、乙两组数据稳定性的描述,正确的是( ) 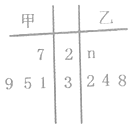
A.甲较稳定
B.乙较稳定
C.二者相同
D.无法判断
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2sin Acos C=2sin B-sin C.
(1)求A的大小;
(2)在锐角三角形ABC中, ![]() ,求c+b的取值范围.
,求c+b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com