
【题目】关于函数![]() ,
,![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.当![]() 时,
时,![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
B.当![]() 时,
时,![]() 存在唯一极小值点
存在唯一极小值点![]() ,且
,且![]()
C.对任意![]() ,
,![]() 在
在![]() 上均存在零点
上均存在零点
D.存在![]() ,
,![]() 在
在![]() 上有且只有一个零点
上有且只有一个零点
【答案】ABD
【解析】
当![]() 时,
时,![]() ,求出
,求出![]() ,得到
,得到![]() 在
在![]() 处的切线的点斜式方程,即可判断选项A;求出
处的切线的点斜式方程,即可判断选项A;求出![]() 的解,确定
的解,确定![]() 单调区间,进而求出
单调区间,进而求出![]() 极值点个数,以及极值范围,可判断选项B;令
极值点个数,以及极值范围,可判断选项B;令![]() ,当
,当![]() 时,分离参数可得
时,分离参数可得![]() ,设
,设![]() ,求出
,求出![]() 的极值最值,即可判断选项C,D的真假.
的极值最值,即可判断选项C,D的真假.
当![]() 时,
时,![]() ,
,
![]() ,
,
所以![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() ,所以选项A正确;
,所以选项A正确;
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 单调递增,
单调递增,
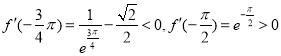
所以存在![]() ,使得
,使得![]() ,
,
当![]() ,
,
所以![]() 是
是![]() 唯一极小值点,且
唯一极小值点,且![]() ,
,
![]() ,
,
![]() ,
,
![]() ,所以选项B正确;
,所以选项B正确;
令![]() ,当
,当![]() 时,
时,![]() ,
,
设![]() ,
,
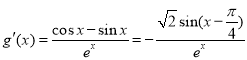 ,
,
令![]() ,
,
由![]() 图像可知,
图像可知,
当![]() 时
时![]() 取极大值,又
取极大值,又![]() ,
,
 ,
,
当![]() 时
时![]() 极小值,又
极小值,又![]() ,
,
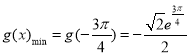 ,
,

所以当![]() ,
,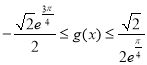 ,
,
当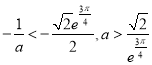 时,
时,
![]() 与直线
与直线![]() 没有交点,
没有交点,
即![]() 在
在![]() 上不存在零点,所以选项C错误;
上不存在零点,所以选项C错误;
当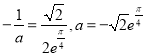 时,
时,![]() 与直线
与直线![]() 有唯一交点,
有唯一交点,
此时![]() 在
在![]() 上有且只有一个零点,所以选项D正确.
上有且只有一个零点,所以选项D正确.
故选:ABD.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了比较两位运动员甲和乙的打靶成绩,在相同条件下测得各打靶![]() 次所得环数(已按从小到大排列)如下:
次所得环数(已按从小到大排列)如下:
甲的环数:![]()
乙的环数:![]()
(1)完成茎叶图,并分别计算两组数据的平均数及方差;

(2)(i)根据(1)的结果,分析两人的成绩;
(ii)如果你是教练,请你作出决策:根据对手实力的强弱分析应该派两人中的哪一位上场比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点P(-4,0)的动直线l与抛物线![]() 相交于D、E两点,已知当l的斜率为
相交于D、E两点,已知当l的斜率为![]() 时,
时,![]() .
.
(1)求抛物线C的方程;
(2)设![]() 的中垂线在
的中垂线在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到![]() 距离的最大值及该点坐标.
距离的最大值及该点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且焦距为4
,且焦距为4
(1)求椭圆![]() 的标准方程:
的标准方程:
(2)设![]() 为直线
为直线![]() 上一点,
上一点,![]() 为椭圆
为椭圆![]() 上一点.以
上一点.以![]() 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点![]() .
.
(i)求![]() 的取值范围
的取值范围
(ii)是否存在圆心在原点的定圆恒与直线![]() 相切?若存在,求出该定圆的方程;若不存在,说明理由.
相切?若存在,求出该定圆的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从广安市某中学校的![]() 名男生中随机抽取
名男生中随机抽取![]() 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于![]() cm和
cm和![]() cm之间,将测量结果按如下方式分成八组:第一组
cm之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,...,第八组
,...,第八组![]() ,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为![]() 人.
人.
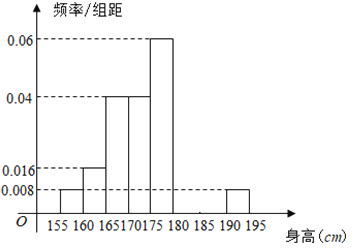
(1)求第七组的频率;
(2)估计该校![]() 名男生的身高的中位数。
名男生的身高的中位数。
(3)若从样本中身高属于第六组和第八组的所有男生中随机抽取两名男生,求抽出的两名男生是同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com