
【题目】已知函数![]() 是奇函数.
是奇函数.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
【答案】(1)![]() ;
;
(2)函数![]() 是单调递增函数;
是单调递增函数;
(3)![]() 时,值域为:
时,值域为:![]() ;
;![]() 时,值域为:
时,值域为:![]() .
.
【解析】
(1)由函数![]() 是奇函数,利用函数的定义域为
是奇函数,利用函数的定义域为![]() 时,奇函数在0处有定义,则
时,奇函数在0处有定义,则![]() 即可解的
即可解的![]() 的值;
的值;
(2)由题意利用函数的单调性的定义加以证明函数的单调性,;
(3)由题意先求出函数![]() 的值域,令函数
的值域,令函数![]() 为
为![]() 利用“对勾”函数的单调性求出定义域下的函数的值域.
利用“对勾”函数的单调性求出定义域下的函数的值域.
(1)因为函数![]() 定义域为
定义域为![]() 且函数
且函数![]() 是奇函数,
是奇函数,![]() ,
,
(2) 函数![]() 是单调递增函数.证明如下:
是单调递增函数.证明如下:
由(1)得![]() ,因为定义域为
,因为定义域为![]() , 所以任取
, 所以任取![]() ,且
,且![]() ,
,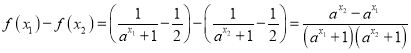 ,
,![]()
![]()
![]()
![]() ,又
,又![]() ,
, ,所以
,所以![]() ,
,![]() 是单调递增函数;
是单调递增函数;
(3)由(2)得,![]() 是单调递增函数,所以
是单调递增函数,所以![]() 时,
时,![]() ,所以
,所以![]() ,
,
所以令![]() ,
,
任取![]() ,且
,且![]() ,
,
则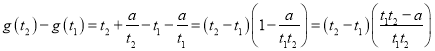 ,
,
因为![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,
所以当![]() 时,
时,![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 时,
时,![]() ,而
,而![]() 时,
时,![]() ,
,
即![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增;
单调递增;
所以当![]() 时,
时, 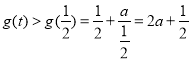 ,
,
即当![]() 时,函数
时,函数![]() 的值域为:
的值域为:![]()
当![]() 时,
时,![]() ,
,
即当![]() 时,函数
时,函数![]() 的值域为:
的值域为:![]() .
.
综上可得:
![]() 时,函数
时,函数![]() 的值域为:
的值域为:![]() .
.
![]() 时,函数
时,函数![]() 的值域为:
的值域为:![]() ;
;
故得解.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】先后2次抛掷一次骰子,将得到的点数分别记为![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形(含等边三角形)的概率.
,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形(含等边三角形)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2018年第一季度五省GDP情况图,则下列描述中不正确的是( )

A. 与去年同期相比2018年第一季度五个省的GDP总量均实现了增长
B. 2018年第一季度GDP增速由高到低排位第5的是浙江省
C. 2018年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D. 去年同期河南省的GDP总量不超过4000亿元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() .
.
(1)若抛物线![]() 的焦点到准线的距离为4,直线
的焦点到准线的距离为4,直线![]() ,求直线
,求直线![]() 截抛物线
截抛物线![]() 所得的弦长;
所得的弦长;
(2)过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,过点
两点,过点![]() 作抛物线的切线,两切线相交于点
作抛物线的切线,两切线相交于点![]() ,若
,若![]() 分别表示直线
分别表示直线![]() 与直线
与直线![]() 的斜率,且
的斜率,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程及直线
的方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若A∪B=A,求实数m的取值范围;
(2)当x∈Z时,求A的非空真子集的个数;
(3)当x∈R时,若A∩B=,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com