
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,二面角
,二面角![]() 为
为![]() .
.
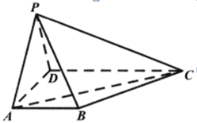
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)证明![]() 平面
平面![]() 可得
可得![]() ,且
,且![]() 为二面角
为二面角![]() 的平面角,计算出
的平面角,计算出![]() ,可根据勾股定理得出
,可根据勾股定理得出![]() ,可得
,可得![]() 平面
平面![]() .
.
(2)建立空间坐标系,求出平面![]() 的法向量
的法向量![]() ,则
,则![]() 为直线
为直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
解:(1)因为平面![]() 平面
平面![]()
平面![]() 平面
平面![]() ,
,![]() 面
面![]() ,
,![]() .
.
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
,
所以![]() 即为二面角
即为二面角![]() 的平面角,所以
的平面角,所以![]() ,
,
又因为在![]() 中,
中,![]() ,
,![]() ,由余弦定理得
,由余弦定理得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)在平面![]() 内过点
内过点![]() 作
作![]() .垂足为
.垂足为![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,以
,以![]() 为坐标原点,建立如图所示的空间直角坐标系.
为坐标原点,建立如图所示的空间直角坐标系.
因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,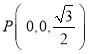 ,
,![]() ,
,![]() ,
,
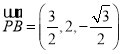 ,
, ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
所以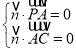 ,即
,即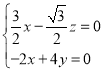 ,
,
取![]() ,则平面
,则平面![]() 的一个法向量为
的一个法向量为![]() .
.
记直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则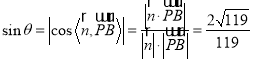 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A. 288种 B. 144种 C. 720种 D. 360种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() 平面ABCD,底面ABCD是等腰梯形,
平面ABCD,底面ABCD是等腰梯形,![]() ,
,![]() .
.
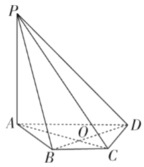
(1)证明:![]() 平面PAC;
平面PAC;
(2)若![]() ,
,![]() ,设
,设![]() ,且
,且![]() ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》的盈不足章第19个问题中提到:“今有良马与驽马发长安,至齐.齐去长安三千里.良马初日行一百九十三里,日增一十三里.驽马初日行九十七里,日减半里…”其大意为:“现在有良马和驽马同时从长安出发到齐去.已知长安和齐的距离是3000里.良马第一天行193里,之后每天比前一天多行13里.驽马第一天行97里,之后每天比前一天少行0.5里…”试问前4天,良马和驽马共走过的路程之和的里数为( )

A.1235B.1800C.2600D.3000
查看答案和解析>>
科目:高中数学 来源: 题型:
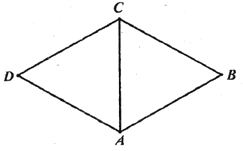
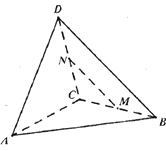
【题目】![]() 分别为菱形
分别为菱形![]() 的边
的边![]() 的中点,将菱形沿对角线
的中点,将菱形沿对角线![]() 折起,使点
折起,使点![]() 不在平面
不在平面![]() 内,则在翻折过程中,以下命题正确的是___________.(写出所有正确命题的序号)
内,则在翻折过程中,以下命题正确的是___________.(写出所有正确命题的序号)
①![]() 平面
平面![]() ;②异面直线
;②异面直线![]() 与
与![]() 所成的角为定值;③在二面角
所成的角为定值;③在二面角![]() 逐渐渐变小的过程中,三棱锥
逐渐渐变小的过程中,三棱锥![]() 的外接球半径先变小后变大;④若存在某个位程,使得直线
的外接球半径先变小后变大;④若存在某个位程,使得直线![]() 与直线
与直线![]() 垂直,则
垂直,则![]() 的取值范围是
的取值范围是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)设函数![]() 的导函数是
的导函数是![]() ,若不等式
,若不等式![]() 对于任意的实数
对于任意的实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设函数![]() ,
,![]() 是函数
是函数![]() 的导函数,若函数
的导函数,若函数![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com