
ЁОЬтФПЁПТжДЌ![]() ДгФГИлПкНЋвЛаЉЮяЦЗЫЭЕНе§КНааЕФТжДЌ
ДгФГИлПкНЋвЛаЉЮяЦЗЫЭЕНе§КНааЕФТжДЌ![]() ЩЯЃЌдкТжДЌ
ЩЯЃЌдкТжДЌ![]() ГіЗЂЪБЃЌТжДЌ
ГіЗЂЪБЃЌТжДЌ![]() ЮЛгкИлПк
ЮЛгкИлПк![]() ББЦЋЮї
ББЦЋЮї![]() Чвгы
Чвгы![]() ЯрОр20КЃРяЕФ
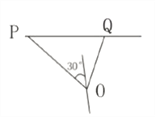
ЯрОр20КЃРяЕФ![]() ДІЃЌВЂе§вд30КЃРяЕФКНЫйбие§ЖЋЗНЯђдШЫйааЪЛЃЌМйЩшТжДЌ
ДІЃЌВЂе§вд30КЃРяЕФКНЫйбие§ЖЋЗНЯђдШЫйааЪЛЃЌМйЩшТжДЌ![]() бижБЯпЗНЯђвд
бижБЯпЗНЯђвд![]() КЃРя/аЁЪБЕФКНЫйдШЫйааЪЛЃЌОЙ§
КЃРя/аЁЪБЕФКНЫйдШЫйааЪЛЃЌОЙ§![]() аЁЪБгыТжДЌ
аЁЪБгыТжДЌ![]() Яргі.
Яргі.
ЃЈ1ЃЉШєЪЙЯргіЪБТжДЌ![]() КНОрзюЖЬЃЌдђТжДЌ
КНОрзюЖЬЃЌдђТжДЌ![]() ЕФКНааЫйЖШДѓаЁгІЮЊЖрЩйЃП
ЕФКНааЫйЖШДѓаЁгІЮЊЖрЩйЃП
ЃЈ2ЃЉМйЩшТжДЌ![]() ЕФзюИпКНЫйжЛФмДяЕН30КЃРя/аЁЪБЃЌдђТжДЌ
ЕФзюИпКНЫйжЛФмДяЕН30КЃРя/аЁЪБЃЌдђТжДЌ![]() вдЖрДѓЫйЖШМАЪВУДКНааЗНЯђВХФмдкзюЖЬЪБМфгыТжДЌ
вдЖрДѓЫйЖШМАЪВУДКНааЗНЯђВХФмдкзюЖЬЪБМфгыТжДЌ![]() ЯргіЃЌВЂЫЕУїРэгЩ.
ЯргіЃЌВЂЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉТжДЌ![]() вд
вд![]() КЃРя/аЁЪБЕФЫйЖШКНааЃЌЯргіЪБТжДЌ
КЃРя/аЁЪБЕФЫйЖШКНааЃЌЯргіЪБТжДЌ![]() КНОрзюЖЬЃЛЃЈ2ЃЉКНЯђЮЊББЦЋЖЋ
КНОрзюЖЬЃЛЃЈ2ЃЉКНЯђЮЊББЦЋЖЋ![]() ЃЌКНЫйЮЊ30КЃРя/аЁЪБЃЌТжДЌ
ЃЌКНЫйЮЊ30КЃРя/аЁЪБЃЌТжДЌ![]() ФмдкзюЖЬЪБМфгыТжДЌ
ФмдкзюЖЬЪБМфгыТжДЌ![]() Яргі.
Яргі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшСНТжДЌдк![]() ДІЯргіЃЌдк
ДІЯргіЃЌдк![]() жаЃЌРћгУгрЯвЖЈРэЕУГі
жаЃЌРћгУгрЯвЖЈРэЕУГі![]() ЙигкtЕФКЏЪ§ЃЌДгЖјЕУГі
ЙигкtЕФКЏЪ§ЃЌДгЖјЕУГі![]() ЕФзюаЁжЕМАЦфЖдгІЕФ
ЕФзюаЁжЕМАЦфЖдгІЕФ![]() ЃЌЕУГіЫйЖШЃЛ
ЃЌЕУГіЫйЖШЃЛ
ЃЈ2ЃЉРћгУгрЯвЖЈРэМЦЫуКНааЪБМф![]() ЃЌЕУГі
ЃЌЕУГі![]() ОрРыЃЌДгЖјЕУГі
ОрРыЃЌДгЖјЕУГі![]() ЕФЖШЪ§ЃЌЕУГіКНааЗНАИЃЎ
ЕФЖШЪ§ЃЌЕУГіКНааЗНАИЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЩшЯргіЪБТжДЌ![]() КНааЕФОрРыЮЊ
КНааЕФОрРыЮЊ![]() КЃРяЃЌдђ
КЃРяЃЌдђ
![]()
![]()
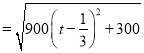 .
.
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌ
ЃЌ 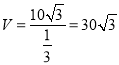 ЃЌ
ЃЌ
МДТжДЌ![]() вд
вд![]() КЃРя/аЁЪБЕФЫйЖШКНааЃЌЯргіЪБТжДЌ
КЃРя/аЁЪБЕФЫйЖШКНааЃЌЯргіЪБТжДЌ![]() КНОрзюЖЬ.
КНОрзюЖЬ.
ЃЈ2ЃЉЩшТжДЌ![]() гыТжДЌ
гыТжДЌ![]() дк
дк![]() ДІЯргіЃЌдђ
ДІЯргіЃЌдђ![]()
![]() ЃЌ
ЃЌ
МД![]() .
.
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌгж
ЃЌгж![]() ЪБ
ЪБ![]() ЃЌ
ЃЌ
Ёр![]() ЪБЃЌ
ЪБЃЌ ![]() зюаЁЧвЮЊ
зюаЁЧвЮЊ![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() жа
жа![]() ЃЌ
ЃЌ
ЁрКНЯђЮЊББЦЋЖЋ![]() ЃЌКНЫйЮЊ30КЃРя/аЁЪБЃЌ
ЃЌКНЫйЮЊ30КЃРя/аЁЪБЃЌ
ТжДЌ![]() ФмдкзюЖЬЪБМфгыТжДЌ
ФмдкзюЖЬЪБМфгыТжДЌ![]() Яргі.
Яргі.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊе§ЫФУцЬх![]() ЕФРтГЄЮЊ
ЕФРтГЄЮЊ![]() ЃЌ
ЃЌ![]() ЮЊРт
ЮЊРт![]() ЕФжаЕуЃЌЙ§
ЕФжаЕуЃЌЙ§![]() зїЦфЭтНгЧђЕФНиУцЃЌдђНиУцУцЛ§ЕФзюаЁжЕЮЊ__________ЃЎ
зїЦфЭтНгЧђЕФНиУцЃЌдђНиУцУцЛ§ЕФзюаЁжЕЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєвЛЯЕСаКЏЪ§ЕФНтЮіЪНКЭжЕгђЯрЭЌЃЌЕЋЪЧЖЈвхгђВЛЭЌЃЌдђГЦетаЉКЏЪ§ЮЊЁАЭЌзхКЏЪ§ЁБЃЌР§ШчКЏЪ§y=x2 ЃЌ xЁЪ[1ЃЌ2]ЃЌгыКЏЪ§y=x2 ЃЌ xЁЪ[Љ2ЃЌЉ1]МДЮЊЁАЭЌзхКЏЪ§ЁБЃЎЯТУцЕФКЏЪ§НтЮіЪНвВФмЙЛБЛгУРДЙЙдьЁАЭЌзхКЏЪ§ЁБЕФЪЧЃЈ ЃЉ
A.y=x
B.y=|xЉ3|
C.y=2x
D.y=log ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊМЏКЯA={x|ЃЈxЉaЃЉ[xЉЃЈa+3ЃЉ]Ём0}ЃЈaЁЪRЃЉЃЌB={x|x2Љ4xЉ5ЃО0}ЃЎ
ЃЈ1ЃЉШєAЁЩB=ЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєAЁШB=BЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖЈвхдкRЩЯЕФКЏЪ§fЃЈxЃЉЃЌЖдШЮвтaЃЌbЁЪRЃЌЖМгаfЃЈa+bЃЉ=fЃЈaЃЉ+fЃЈbЃЉЉ1ЃЌЕБxЃО0ЪБЃЌfЃЈxЃЉЃО1ЃЛЧвfЃЈ2ЃЉ=3ЃЌ
ЃЈ1ЃЉЧѓfЃЈ0ЃЉМАfЃЈ1ЃЉЕФжЕЃЛ
ЃЈ2ЃЉХаЖЯКЏЪ§fЃЈxЃЉдкRЩЯЕФЕЅЕїадЃЌВЂИјгшжЄУїЃЛ
ЃЈ3ЃЉШєfЃЈЉkx2ЃЉ+fЃЈkxЉ2ЃЉЃМ2ЖдШЮвтЕФxЁЪRКуГЩСЂЃЌЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаИїЪНжаЃЌе§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
Ђй={0}ЃЛЂк{0}ЃЛЂлЁЪ{0}ЃЛЂм0={0}ЃЛЂн0ЁЪ{0}ЃЛЂо{1}ЁЪ{1ЃЌ2ЃЌ3}ЃЛЂп{1ЃЌ2}{1ЃЌ2ЃЌ3}ЃЛЂр{aЃЌb}={bЃЌa}ЃЎ
A.1
B.2
C.3
D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЭждВ![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌвдЭждВ
ЃЌвдЭждВ![]() ЕФЩЯЖЅЕу
ЕФЩЯЖЅЕу![]() ЮЊдВаФзїдВЃЌ
ЮЊдВаФзїдВЃЌ
![]() ЃЌдВ
ЃЌдВ![]() гыЭждВ
гыЭждВ![]() дкЕквЛЯѓЯоНЛгкЕу
дкЕквЛЯѓЯоНЛгкЕу![]() ,дкЕкЖўЯѓЯоНЛгкЕу
,дкЕкЖўЯѓЯоНЛгкЕу![]() .
.
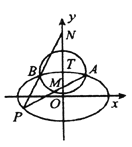
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФзюаЁжЕЃЌВЂЧѓГіДЫЪБдВ
ЕФзюаЁжЕЃЌВЂЧѓГіДЫЪБдВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ3ЃЉЩшЕу![]() ЪЧЭждВ
ЪЧЭждВ![]() ЩЯвьгк
ЩЯвьгк![]() ЕФвЛЕуЃЌЧвжБЯп
ЕФвЛЕуЃЌЧвжБЯп![]() ЗжБ№гы
ЗжБ№гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЮЊзјБъдЕуЃЌЧѓжЄ:
ЮЊзјБъдЕуЃЌЧѓжЄ:
![]() ЮЊЖЈжЕ.
ЮЊЖЈжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШєХзЮяЯпЕФНЙЕуЪЧЭждВ![]() зѓЖЅЕуЃЌЧѓДЫХзЮяЯпЕФБъзМЗНГЬЃЛ
зѓЖЅЕуЃЌЧѓДЫХзЮяЯпЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉШєФГЫЋЧњЯпгыЭждВ![]() ЙВНЙЕуЃЌЧввд
ЙВНЙЕуЃЌЧввд![]() ЮЊНЅНќЯпЃЌЧѓДЫЫЋЧњЯпЕФБъзМЗНГЬЃЎ
ЮЊНЅНќЯпЃЌЧѓДЫЫЋЧњЯпЕФБъзМЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГОЯњЩЬДгЭтЕивЛЫЎжГГЇЙКНјвЛХњаЁСњЯКЃЌВЂЫцЛњГщШЁ40жЛНјааЭГМЦЃЌАДжиСПЗжРрЭГМЦНсЙћШчЯТЭМЃК
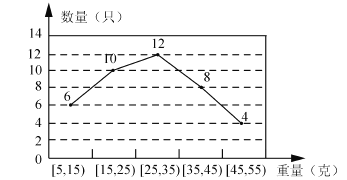
ЃЈ1ЃЉМЧЪТМў![]() ЮЊЃКЁАДгетХњаЁСњЯКжаШЮШЁвЛжЛЃЌжиСПВЛГЌЙ§35
ЮЊЃКЁАДгетХњаЁСњЯКжаШЮШЁвЛжЛЃЌжиСПВЛГЌЙ§35![]() ЕФаЁСњЯКЁБЃЌЧѓ
ЕФаЁСњЯКЁБЃЌЧѓ![]() ЕФЙРМЦжЕЃЛ
ЕФЙРМЦжЕЃЛ
ЃЈ2ЃЉЪдЙРМЦетХњаЁСњЯКЕФЦНОљжиСПЃЛ
ЃЈ3ЃЉЮЊЪЪгІЪаГЁашЧѓЃЌжЦЖЈДйЯњВпТдЃЎИУОЯњЩЬгжНЋетХњаЁСњЯКЗжГЩШ§ИіЕШМЖЃЌВЂжЦЖЈГіЯњЪлЕЅМлЃЌШчЯТБэЃК
ЕШМЖ | вЛЕШЦЗ | ЖўЕШЦЗ | Ш§ЕШЦЗ |
жиСПЃЈ |
|
|
|
ЕЅМлЃЈдЊ/жЛЃЉ | 1.2 | 1.5 | 1.8 |
ЪдЙРЫуИУОЯњЩЬвдУПЧЇПЫжСЖрЛЈЖрЩйдЊЃЈШЁећЪ§ЃЉЪеЙКетХњаЁСњЯКЃЌВХФмЛёЕУРћШѓЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com