
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
分析 由出原函数的导函数,得到f′(0),再由两直线垂直与斜率的关系求得m值.
解答 解:由f(x)=ex+$\frac{2x-5}{{x}^{2}+1}$,得f′(x)=${e}^{x}+\frac{2({x}^{2}+1)-2x(2x-5)}{({x}^{2}+1)^{2}}={e}^{x}+\frac{-2{x}^{2}+10x+2}{({x}^{2}+1)^{2}}$,
则f′(0)=e0+2=3,
∵函数f(x)=ex+$\frac{2x-5}{{x}^{2}+1}$的图象在点(0,f(0))处的切线与直线x-my+4=0垂直,
∴$\frac{1}{m}=-\frac{1}{3}$,则m=-3.
故选:A.
点评 本题考查利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.


科目:高中数学 来源: 题型:选择题
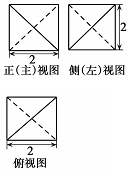
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
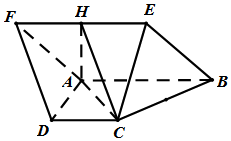 如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点
如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y-1=0 | B. | x-y=0 | C. | x-y-$\sqrt{3}$=0 | D. | x-y-2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 模型1 | B. | 模型2 | C. | 模型3 | D. | 模型4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com