
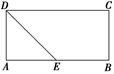
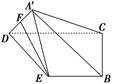
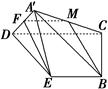
如图,在矩形ABCD中,AB=4,AD=2,E为AB的中点,现将△ ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCDE,F为线段A′D的中点.
(1)求证:EF//平面A′BC;
(2)求直线A′B与平面A′DE所成角的正切值.
(1)要证明线面平行,只要通过证明线线平行来得到即可。
(2)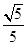
【解析】
试题分析:解:(1)证明:取A′C的中点M,连结MF,MB,则FM∥DC,且FM=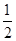 DC.
DC.
∵EB∥DC,且EB=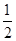 DC,
DC,
∴FM∥EB且FM=EB.
∴四边形EBMF为平行四边形,
∴EF∥MB.
∵EF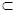 平面A′BC,MB
平面A′BC,MB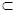 平面A′BC,
平面A′BC,
∴EF∥平面A′BC. 4分
(2)过B作BO垂直于DE的延长线,O为垂足,连结A′O.
∵平面A′DE⊥平面BCDE,且平面A′DE∩平面BCDE=DE,
∴BO⊥平面A′DE,
∴∠BA′O就是直线A′B与平面A′DE所成的角. 7分
过A′作A′S⊥DE,S为垂足,
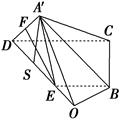
因为平面A′DE⊥平面BCDE,且平面A′DE∩平面BCDE=DE,
所以A′S⊥平面BCDE.
在Rt△A′SO中,A′S=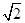 ,SO=2
,SO=2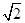 ,所以A′O=
,所以A′O=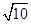 .
.
又BO=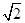 ,所以tan∠BA′O=
,所以tan∠BA′O=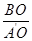 =
=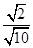 =
=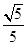 ,
,
故直线A′B与平面A′DE所成角的正切值为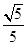 .
10分
.
10分
考点:直线与平面平行的判定定理
点评:本题主要考查了直线与平面平行的判定定理与线面平行与线线平行的相互转化,还考查了直线与平面所成角的求解,要注意利用已知图形构造直角三角形进行求解.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.
如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.
如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com