
【题目】设函数![]() .
.
(I)当a=1时,证明![]() 在
在![]() 是增函数;
是增函数;
(Ⅱ)若当![]() 时,
时,![]() ,求a取值范围.
,求a取值范围.
【答案】(I)见解析(Ⅱ)![]()
【解析】
(Ⅰ)当a=1时,求得f′(x)![]() (x>0).令g(x)=ex﹣1﹣x,求出g(x)的导函数,分析g(x)的单调性,求得g(x)有最小值0,从而可得g(x)≥0,即f′(x)≥0,则f(x)在(0,+∞)是增函数;
(x>0).令g(x)=ex﹣1﹣x,求出g(x)的导函数,分析g(x)的单调性,求得g(x)有最小值0,从而可得g(x)≥0,即f′(x)≥0,则f(x)在(0,+∞)是增函数;
(Ⅱ)设h(x)=f(x+1)=ln(x+1)+ae﹣x﹣a(x>0),求其导函数,得h′(x)![]() .令p(x)=ex﹣a(x+1),对a分类分析p(x)的符号,得到h(x)的单调性,从而求得满足f(x+1)>0时a的取值范围.
.令p(x)=ex﹣a(x+1),对a分类分析p(x)的符号,得到h(x)的单调性,从而求得满足f(x+1)>0时a的取值范围.
(Ⅰ)当a=1时,f′(x)![]() (x>0).
(x>0).
令g(x)=ex﹣1﹣x,g′(x)=ex﹣1﹣1,
由g′(x)=0,可得x=1.
当x∈(0,1)时,g′(x)<0,g(x)单调递减,
当x∈(1,+∞)时,g′(x)>0,g(x)单调递增,
∴当x=1时,g(x)min=g(1)=0,即g(x)≥0,
∴f′(x)≥0,则f(x)在(0,+∞)是增函数;
(Ⅱ)解:设h(x)=f(x+1)=ln(x+1)+ae﹣x﹣a(x>0),
h′(x)![]() .
.
令p(x)=ex﹣a(x+1),则p′(x)=ex﹣a.
①当a≤1时,p′(x)>e0﹣a=1﹣a≥0,
∴p(x)在(0,+∞)上单调递增,
∴p(x)>p(0)=1﹣a≥0.
∴h′(x)>0,
∴h(x)在(0,+∞)上单调递增,
则h(x)>h(0)=0,结论成立;
②当a>1时,由p′(x)=0,可得x=lna,
当x∈(0,lna)时,p′(x)<0,p(x)单调递减,
又p(0)=1﹣a<0,
∴x∈(0,lna)时,p(x)<0恒成立,
即h′(x)<0.
∴x∈(0,lna)时,h(x)单调递减,
此时h(x)<h(0)=0,结论不成立.
综上,a≤1.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,短轴的两端点分别为
,短轴的两端点分别为![]() ,
,![]() ,线段
,线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,且四边形
,且四边形![]() 是面积为8的矩形.
是面积为8的矩形.
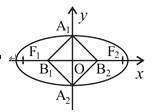
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 到点
到点![]() ,
, ![]() 及到直线
及到直线![]() 的距离都相等,如果这样的点恰好只有一个,那么实数
的距离都相等,如果这样的点恰好只有一个,那么实数![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
【答案】D
【解析】试题分析:由题意知![]() 在抛物线
在抛物线![]() 上,设
上,设 ,则有
,则有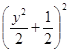
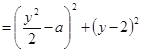 ,化简得
,化简得![]() ,当
,当![]() 时,符合题意;当
时,符合题意;当![]() 时,
时,![]() ,有
,有![]() ,
,![]() ,则
,则![]() ,所以选D.
,所以选D.
考点:1、点到直线的距离公式;2、抛物线的性质.
【方法点睛】本题考查抛物线的概念、性质以及数形结合思想,属于中档题,到点![]() 和直线
和直线![]() 的距离相等,则
的距离相等,则![]() 的轨迹是抛物线,再由直线与抛物线的位置关系可求;抛物线的定义是解决物线问题的基础,它能将两种距离(抛物线上的点到到焦点的距离、抛物线上的点到准线的距离)进行等量转化,如果问题中涉及抛物线的焦点和准线,又能与距离联系起来,那么用抛物线的定义就能解决.
的轨迹是抛物线,再由直线与抛物线的位置关系可求;抛物线的定义是解决物线问题的基础,它能将两种距离(抛物线上的点到到焦点的距离、抛物线上的点到准线的距离)进行等量转化,如果问题中涉及抛物线的焦点和准线,又能与距离联系起来,那么用抛物线的定义就能解决.
【题型】单选题
【结束】
13
【题目】在极坐标系中,已知两点![]() ,
, ![]() ,则
,则![]() ,
, ![]() 两点间的距离为__________.
两点间的距离为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数,
是参数,![]() ),直线
),直线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),曲线
是参数),曲线![]() 与直线
与直线![]() 有一个公共点在
有一个公共点在![]() 轴上,以坐标原点为极点,
轴上,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系
轴的非负半轴为极轴建立极坐标系
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若点![]() ,
,![]() ,
,![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com