
【题目】下列是有关三角形ABC的几个命题,
①若tanA+tanB+tanC>0,则△ABC是锐角三角形;
②若sin2A=sin2B,则△ABC是等腰三角形;
③若( ![]() +
+ ![]() )
) ![]() =0,则△ABC是等腰三角形;
=0,则△ABC是等腰三角形;
④若cosA=sinB,则△ABC是直角三角形;
其中正确命题的个数是( )
A..1
B..2
C.3
D.4
【答案】B
【解析】解:①∵tanA+tanB=tan(A+B)(1﹣tanAtanB),
∴tanA+tanB+tanC=tan(A+B)(1﹣tanAtanB)+tanC=tanAtanBtanC>0,
∴A,B,C是△ABC的内角,故内角都是锐角,故①正确;
②∵sin2A=sin2B
∴sin2A﹣sin2B=cos(A+B)sin(A﹣B)=0
∴cos(A+B)=0或sin(A﹣B)=0
∴A+B= ![]() 或A=B,
或A=B,
若sin2A=sin2B,则△ABC是等腰三角形或是直角三角形;故②错误
③若( ![]() +
+ ![]() )
) ![]() =0,
=0,
则( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=0,
)=0,
即| ![]() |2﹣|
|2﹣| ![]() |2=0,
|2=0,
则| ![]() |2=|
|2=| ![]() |2 , 即|
|2 , 即| ![]() |=|
|=| ![]() |,
|,
则AB=AC,则△ABC是等腰三角形;正确,故③正确,
④若cosA=sinB,则sinB=cosA=sin( ![]() ),∴
),∴ ![]() ,
,
即A+B= ![]() 或B﹣A=
或B﹣A= ![]() ,则△ABC不一定为直角三角形,故④错误,
,则△ABC不一定为直角三角形,故④错误,
故选:B
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】如图,记长方体ABCD﹣A1B1C1D1被平行于棱B1C1的平面EFGH截去右上部分后剩下的几何体为Ω,则下列结论中不正确的是( ) 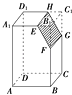
A.EH∥FG
B.四边形EFGH是平行四边形
C.Ω是棱柱
D.Ω是棱台
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,且点
,且点 ![]() 在该椭圆上
在该椭圆上
(1)求椭圆C的方程;
(2)过椭圆C的左焦点F1的直线l与椭圆相交于A,B两点,若△AOB的面积为 ![]() ,求圆心在原点O且与直线l相切的圆的方程.
,求圆心在原点O且与直线l相切的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)对任意x∈R,都有f(﹣x)+f(x)=0,f(x)+f(x+
sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)对任意x∈R,都有f(﹣x)+f(x)=0,f(x)+f(x+ ![]() )=0,则f(
)=0,则f( ![]() )=( )
)=( )
A.0
B.1
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1 , BC的中点. 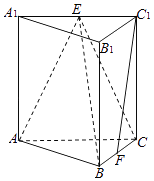
(1)求证:AB⊥C1F;
(2)求证:C1F∥平面ABE;
(3)求三棱锥E﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(cosx,sinx),x∈R,函数f(x)=
=(cosx,sinx),x∈R,函数f(x)= ![]() (
( ![]() ﹣
﹣ ![]() ).
).
(1)求函数f(x)的最小正周期;
(2)当x∈[- ![]() ,
, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下四种变换方式:
① 向左平移![]() 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的![]() ;
;
② 向右平移![]() 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的![]() ;
;
③ 每个点的横坐标缩短为原来的![]() ,向右平移
,向右平移![]() 个单位长度;
个单位长度;
④ 每个点的横坐标缩短为原来的![]() ,向左平移
,向左平移![]() 个单位长度;
个单位长度;
其中能将![]() 的图像变换成函数
的图像变换成函数![]() 的图像的是( )
的图像的是( )
A.①和③ B.①和④ C.②和④ D.②和③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() ),且对任意
),且对任意![]() ,都有
,都有![]() .
.
(Ⅰ)用含![]() 的表达式表示
的表达式表示![]() ;
;
(Ⅱ)若![]() 存在两个极值点
存在两个极值点![]() ,
, ![]() ,且
,且![]() ,求出
,求出![]() 的取值范围,并证明
的取值范围,并证明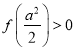 ;
;
(Ⅲ)在(Ⅱ)的条件下,判断![]() 零点的个数,并说明理由.
零点的个数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com