B
分析:由条件利用正弦定理可得 A=B,CB=AC,把A=B代入 AC•cosA=CB•cosB 可得 AC=CB,从而可得在△ABC为等边三角形,设△ABC边长为x,则由条件可得x•x•cos60°=1,求出x的值即为所求.
解答:由题意可得AB•AC•cosA=AB•CB•cosB,
∴AC•cosA=CB•cosB.
再由正弦定理可得sinBcosA=sinAcosB,sin(A-B)=0,∴A=B,∴CB=AC.
把A=B代入 AC•cosA=CB•cosB 可得AC=CB,从而可得在△ABC为等边三角形.
设△ABC边长为x,则由条件可得x•x•cos60°=1,∴x=

,
故选B.
点评:本题主要考查两个向量的数量积的定义,正弦定理的应用,判断△ABC为等边三角形,是解题的关键,属于中档题.

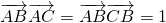 ,则|
,则| |的值为
|的值为

 ,
,

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案