
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 为等边三角形,
为等边三角形,
![]() 且
且![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
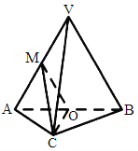
(I)求证:![]() 平面
平面![]() ;
;
(II)求证:平面![]() 平面
平面![]() ;
;
(III)求三棱锥![]() 的体积.
的体积.
【答案】(I)详见解析(II)详见解析(III)![]()
【解析】
试题分析:(Ⅰ)利用三角形的中位线得出OM∥VB,利用线面平行的判定定理证明VB∥平面MOC;(Ⅱ)证明OC⊥平面VAB,即可证明平面MOC⊥平面VAB;(Ⅲ)利用等体积法求三棱锥A-MOC的体积即可
试题解析:(Ⅰ)证明:∵O,M分别为AB,VA的中点,
∴OM∥VB,
∵VB平面MOC,OM平面MOC,
∴VB∥平面MOC;
(Ⅱ)证明:∵AC=BC,O为AB的中点,
∴OC⊥AB,
又∵平面VAB⊥平面ABC,平面ABC∩平面VAB=AB,且OC平面ABC,
∴OC⊥平面VAB,
∵OC平面MOC,
∴平面MOC⊥平面VAB
(Ⅲ)在等腰直角三角形![]() 中,
中,![]() ,
,
所以![]() .
.
所以等边三角形![]() 的面积
的面积![]() .
.
又因为![]() 平面
平面![]() ,
,
所以三棱锥![]() 的体积等于
的体积等于![]() .
.
又因为三棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积相等,
的体积相等,
所以三棱锥![]() 的体积为
的体积为![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 的面积最大时,求
的面积最大时,求![]() 的直线方程.
的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆八中大学城校区与本部校区之间的驾车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
| 25 | 30 | 35 | 40 |
频数(次) | 100 | 150 | 200 | 50 |
以这500次驾车单程所需时间的频率代替某人1次驾车单程所需时间的概率.
(1)求![]() 的分布列与
的分布列与![]() ;
;
(2)某天有3位教师独自驾车从大学城校区返回本部校区,记![]() 表示这3位教师中驾车所用时间少于
表示这3位教师中驾车所用时间少于![]() 的人数,求
的人数,求![]() 的分布列与
的分布列与![]() ;
;
(3)下周某天张老师将驾车从大学城校区出发,前往本部校区做一个50分钟的讲座,结束后立即返回大学城校区,求张老师从离开大学城校区到返回大学城校区共用时间不超过120分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间及所有零点;
的单调区间及所有零点;
(2)设![]() ,
,![]() ,
,![]() 为函数
为函数![]() 图象上的三个不同点,且
图象上的三个不同点,且
![]() .问:是否存在实数
.问:是否存在实数![]() ,使得函数
,使得函数![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行?若存在,求出所有满足条件的实数
平行?若存在,求出所有满足条件的实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知|a|=4,|b|=8,a与b的夹角是120°.
(1) 计算:① |a+b|,② |4a-2b|;
(2) 当k为何值时,(a+2b)⊥(ka-b)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学共有1000名文科学生参加了该市高三第一次质量检查的考试,其中数学成绩如下表所示:
数学成绩分组 | [50,70) | [70,90) | [90,110) | [110,130) | [130,150] |
人数 | 60 |
| 400 | 360 | 100 |
(Ⅰ)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,年级将采用分层抽样的方法抽取100
名同学进行问卷调查. 甲同学在本次测试中数学成绩为75分,求他被抽中的概率;
(Ⅱ)年级将本次数学成绩75分以下的学生当作“数学学困生”进行辅导,请根据所提供数据估计“数
学学困生”的人数;
(III)请根据所提供数据估计该学校文科学生本次考试的数学平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() R,函数
R,函数![]() =
=![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() >1;
>1;
(2)若关于![]() 的方程
的方程![]() +
+![]() =0的解集中恰有一个元素,求
=0的解集中恰有一个元素,求![]() 的值;
的值;
(3)设![]() >0,若对任意
>0,若对任意![]()
![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com