
【题目】《周髀算经》 是我国古代的天文学和数学著作。其中一个问题的大意为:一年有二十四个节气(如图),每个节气晷长损益相同(即物体在太阳的照射下影子长度的增加量和减少量相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:ー丈等于十尺,一尺等于十寸),则立冬节气的晷长为( )
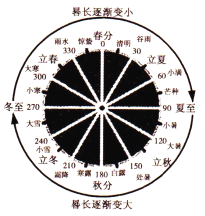
A. 九尺五寸 B. 一丈五寸 C. 一丈一尺五寸 D. 一丈六尺五寸
科目:高中数学 来源: 题型:
【题目】对于实数![]() 符号
符号![]() 表示不超过x的最大整数,例如
表示不超过x的最大整数,例如![]() 定义函数
定义函数![]() 则下列命题正确中的是__________
则下列命题正确中的是__________
(1)函数![]() 的最大值为1;
的最大值为1;
(2)函数![]() 是增函数;
是增函数;
(3)方程![]() 有无数个根;
有无数个根;
(4)函数![]() 的最小值为0.
的最小值为0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,…以此类推:记格点坐标为
,…以此类推:记格点坐标为![]() 的点(
的点(![]() 均为正整数)处所标的数字为
均为正整数)处所标的数字为![]() ,若
,若![]() ,则
,则![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“日行一万步,健康你一生”的养生观念已经深入人心,由于研究性学习的需要,某大学生收集了手机“微信运动”团队中特定甲、乙两个班级![]() 名成员一天行走的步数,然后采用分层抽样的方法按照
名成员一天行走的步数,然后采用分层抽样的方法按照![]() ,
,![]() ,
,![]() ,
,![]() 分层抽取了
分层抽取了![]() 名成员的步数,并绘制了如下尚不完整的茎叶图(单位:千步);已知甲、乙两班行走步数的平均值都是
名成员的步数,并绘制了如下尚不完整的茎叶图(单位:千步);已知甲、乙两班行走步数的平均值都是![]() 千步.
千步.

(1)求![]() ,
,![]() 的值;
的值;
(2)若估计该团队中一天行走步数少于![]() 千步的人数比处于
千步的人数比处于![]() 千步的人数少
千步的人数少![]() 人,求
人,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数有( )
①向量![]() 与
与![]() 是共线向量,则A、B、C、D四点必在一直线上;②单位向量都相等;③任一向量与它的相反向量不相等;④共线的向量,若起点不同,则终点一定不同.
是共线向量,则A、B、C、D四点必在一直线上;②单位向量都相等;③任一向量与它的相反向量不相等;④共线的向量,若起点不同,则终点一定不同.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区工商局、消费者协会在![]() 月
月![]() 号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取
号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取![]() 名群众,按他们的年龄分组:第
名群众,按他们的年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
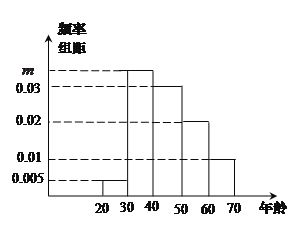
(Ⅰ)若电视台记者要从抽取的群众中选![]() 人进行采访,求被采访人恰好在第
人进行采访,求被采访人恰好在第![]() 组或第
组或第![]() 组的概率;
组的概率;
(Ⅱ)已知第![]() 组群众中男性有
组群众中男性有![]() 人,组织方要从第
人,组织方要从第![]() 组中随机抽取
组中随机抽取![]() 名群众组成维权志愿者服务队,求至少有两名女性的概率.
名群众组成维权志愿者服务队,求至少有两名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ,顺次连接椭圆的四个顶点得到的四边形的面积为
,顺次连接椭圆的四个顶点得到的四边形的面积为![]() ,点
,点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)已知点![]() ,是椭圆
,是椭圆![]() 上的两点.
上的两点.
(ⅰ)若![]() ,且
,且![]() 为等边三角形,求
为等边三角形,求![]() 的面积;
的面积;
(ⅱ)若![]() ,证明:
,证明: ![]() 不可能为等边三角形.
不可能为等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com