
 为偶函数.
为偶函数. 的值;
的值; 有且只有一个根,求实数
有且只有一个根,求实数 的取值范围.
的取值范围. ,(2){a|a>1或a=-2-2
,(2){a|a>1或a=-2-2 }
} .(2)先将方程转化为一元二次方程.由
.(2)先将方程转化为一元二次方程.由 得log4(4x+1)-
得log4(4x+1)- x=log4 (a·2x-a),即
x=log4 (a·2x-a),即 令t=2x,则(1-a)t2+at+1=0,只需其有一正根即可满足题意.①当a=1时,t=-1,不合题意,舍去.②有一正一负根,
令t=2x,则(1-a)t2+at+1=0,只需其有一正根即可满足题意.①当a=1时,t=-1,不合题意,舍去.②有一正一负根, ,a>1. ③有两根相等,a=-2(
,a>1. ③有两根相等,a=-2( +1).
+1). . 6分
. 6分 x=log4 (a·2x-a),
x=log4 (a·2x-a), 8分
8分 ,得a>1.
,得a>1. >0, ∴a>1. ------11分
>0, ∴a>1. ------11分 -2,此时t=
-2,此时t= ,
, -1),则有t=
-1),则有t= <0,此时方程(1-a)t2+at+1=0无正根,
<0,此时方程(1-a)t2+at+1=0无正根, -1)舍去; 13分
-1)舍去; 13分 +1),则有t=
+1),则有t= >0,且a· 2x-a=a(t-1)=a
>0,且a· 2x-a=a(t-1)=a =
= >0,因此a=-2(
>0,因此a=-2( +1). 15分
+1). 15分 }. 16分
}. 16分

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源:不详 题型:解答题
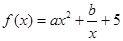
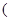 常数
常数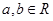 )满足
)满足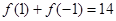 .
.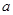 的值,并就常数
的值,并就常数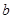 的不同取值讨论函数
的不同取值讨论函数 奇偶性;
奇偶性; 在区间
在区间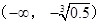 上单调递减,求
上单调递减,求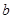 的最小值;
的最小值;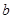 取最小值时,证明:
取最小值时,证明: 恰有一个零点
恰有一个零点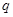 且存在递增的正整数数列
且存在递增的正整数数列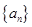 ,使得
,使得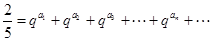 成立.
成立.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,其中a为大于零的常数.
,其中a为大于零的常数. +
+ +…+
+…+ 恒成立.
恒成立. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 为定义域
为定义域 上的单调函数,且存在区间
上的单调函数,且存在区间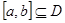 (其中
(其中 ),使得当
),使得当 时,
时, 的取值范围恰为
的取值范围恰为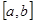 ,则称函数
,则称函数 是
是 上的正函数.若函数
上的正函数.若函数 是
是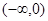 上的正函数,则实数
上的正函数,则实数 的取值范围为( )
的取值范围为( )A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 上两个不同点处的切线重合,则称这条切线为曲线
上两个不同点处的切线重合,则称这条切线为曲线 的“自公切线”.下列方程:①
的“自公切线”.下列方程:① ;②
;②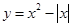 ;③
;③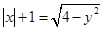 ;④
;④ 对应的曲线中存在“自公切线”的有( )
对应的曲线中存在“自公切线”的有( )| A.①② | B.②③ | C.②④ | D.③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 x ②f:x→y=
x ②f:x→y= x ③f:x→y=
x ③f:x→y= x ④f:x→y=x
x ④f:x→y=x查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com