【题目】[选修44：坐标系与参数方程]
在直角坐标系中
中，曲线
的参数方程为
为参数，
）. 以坐标原点为极点，
轴正半轴为极轴建立极坐标系，已知直线
的极坐标方程为
.
（Ⅰ）求曲线C的普通方程和直线的直角坐标方程；
（Ⅱ）设
是曲线上的一个动点，当
时，求点到直线的距离的最大值.
科目：高中数学 来源： 题型：
【题目】交通指数是指交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念性指数值，记交通指数为
，其范围为
，分别有五个级别：
，畅通；
，基本畅通；
，轻度拥堵；
，中度拥堵；
，严重拥堵.在晚高峰时段（
），从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制的频率分布直方图如图所示.
(1)求出轻度拥堵、中度拥堵、严重拥堵的路段的个数；
(2)用分层抽样的方法从轻度拥堵、中度拥堵、严重拥堵的路段中共抽取6个路段，求依次抽取的三个级别路段的个数；
(3)从(2)中抽取的6个路段中任取2个，求至少有1个路段为轻度拥堵的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在矩形
中
,E为
的中点，将
沿
翻折到
的位置,
平面,
为
的中点,则在翻折过程中，下列结论正确的是( )
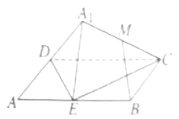
A.恒有
平面
B.B与M两点间距离恒为定值
C.三棱锥
的体积的最大值为
D.存在某个位置，使得平面⊥平面
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在
中，
，
，
，
分别是
，
，
中点，
，
.现将
沿
折起，如图2所示，使二面角
为
，
是的中点.
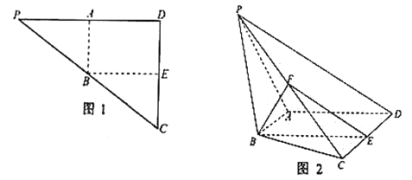
（1）求证：面
面
；
（2）求直线
与平面
所成的角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了比较两种治疗失眠症的药(分别称为
药, 
药)的疗效,随机地选取18位患者服用药,18位患者服用药,这36位患者服用一段时间后,记录他们日平均增加的睡眠时间（单位：
）,试验的观测结果如下:
服用药的18位患者日平均增加的睡眠时间：
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3
服用药的18位患者日平均增加的睡眠时间：
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7
（1）分别计算两组数据的平均数(小数点后保留两位小数),从计算结果看哪种药疗效更好?
（2）根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
已知
是递增数列，其前
项和为
，
，且
，
．
（Ⅰ）求数列的通项
；
（Ⅱ）是否存在
使得
成立？若存在，写出一组符合条件的
的值；若不存在，请说明理由；
（Ⅲ）设
，若对于任意的
，不等式
恒成立，求正整数
的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，
是椭圆上一点.
(1)求椭圆的标准方程；
(2)过椭圆右焦点
的直线与椭圆交于
两点，
是直线
上任意一点.证明：直线
的斜率成等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
