Question

某中学号召本校学生在本学期参加市创办卫生城的相关活动，学校团委对该校学生是否关心创卫活动用简单抽样方法调查了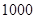位学生（关心与不关心的各一半），

结果用二维等高条形图表示，如图．

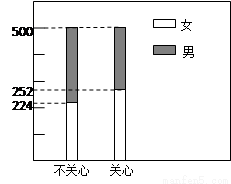
（1）完成列联表，并判断能否有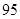℅的把握认为是否关心创卫活动与性别有关？

	0.10	0.05	0.01
	2.706	3.841	6.635

（参考数据与公式：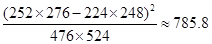

；

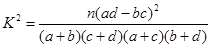	女	男	合计
关心			500
不关心			500
合计		524	1000

 

（2）已知校团委有青年志愿者100名，他们已参加活动的情况记录如下：

参加活动次数	1	2	3
人数	10	50	40

 

（i）从志愿者中任选两名学生，求他们参加活动次数恰好相等的概率；

（ii）从志愿者中任选两名学生，用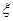表示这两人参加活动次数之差的绝对值，求随机变量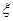的分布列及数学期望．

 

Answer 1

【答案】

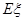（1）不能有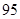℅的把握认为是否关心创卫活动与性别有关．

（2）（i）他们参加活动次数恰好相等的概率为 

(ii) 分布列为

	０	１	２

数学期望：。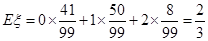

【解析】

试题分析：（1）作出列联表：

	女	男	合计
关心	252	248	500
不关心	224	276	500
合计	476	524	1000

由公式得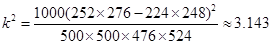 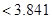           4分

所以不能有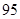℅的把握认为是否关心创卫活动与性别有关．             5分

（2）（i）他们参加活动次数恰好相等的概率为

                                       7分

(ii) 从志愿者中任选两名学生,记“这两人中一人参加1次活动，另一个参加两次活动”为事件，“这两人中一人参加2次活动，另一个参加3次活动”为事件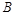，“这两人中一人参加1次活动，另一个参加两次活动”， “这两人中一人参加1次活动，另一个参加3次活动”为事件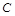．                                 8分

                  9分

                                  10分

分布列为

	０	１	２

数学期望：                     12分

考点：随机变量的分布列及其数学期望，卡方检验。

点评：典型题，统计中的抽样方法，频率直方图，概率计算及分布列问题，是高考必考内容及题型。古典概型概率的计算问题，关键是明确基本事件数，往往借助于“树图法”，做到不重不漏。本题对计算能力要求较高，难度较大。