若函数f(x)=ax3+bx2+cx+d满足f(0)=f(x1)=f(x2)=0(0<x1<x2),且在区间[x2,+∞)上单调递增,则实数b的取值范围是 .
【答案】
分析:由已知,0,x
1,x
2 是函数f(x)=ax
3+bx
2+cx+d的三个零点,可以画出它的大致图象.分两种情况.结合图象分析求解.
解答: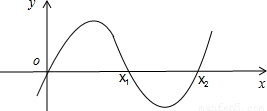
解::∵f(0)=0∴d=0,
∴f(x)=ax
3+bx
2+cx=x(ax
2+bx+c),
又f(x
1)=f(x
2)=0,且0<x
1<x
2,∴x
1,x
2是ax
2+bx+c=0两根,且a≠0.
由韦达定理x
1+x
2=-
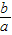
>0,①
当a>0时,f(x)=ax
3+bx
2+cx+d的大致图象为:
由图,符合f(x)在(x
2,+∞)上是增函数,∴a>0满足条件由①得,b<0
当a<0时,f(x)=ax
3+bx
2+cx+d的大致图象为:
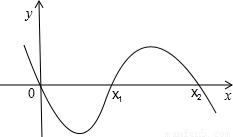
此时f(x)在(x
2,+∞)上不是增函数,不合题意.
故答案为:b<0
点评:本题主要考查了三次函数的图象,及函数单调区间的概念.数形结合的思想方法起到了重要作用.

 解::∵f(0)=0∴d=0,
解::∵f(0)=0∴d=0,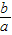 >0,①
>0,①

