
分析 分离参数a,把不等式变形为a≤x+$\frac{36}{x}$+|x2-6x|,只需a小于等于x+$\frac{36}{x}$+|x2-6x|的最小值即可
解答 解:关于x的不等式x2+36+|x3-6x2|≥ax在[2,10]上恒成立,
∴a≤x+$\frac{36}{x}$+|x2-6x|,
而x+$\frac{36}{x}$≥2$\sqrt{x•\frac{36}{x}}$=12,当且仅当x=6∈[2,10]时取等号,
且|x2-6x|≥0,等号当且仅当x=6∈[1,10]时成立;
所以x+$\frac{36}{x}$+|x2-6x||的最小值为12,等号当且仅当x=6∈[2,10]时成立.
故实数a的取值范围是(-∞,12].
故答案为:(-∞,12].
点评 本题主要考查了函数恒成立问题以及绝对值不等式的解法、基本不等式在最值问题中的应用,本题中要注意等号须同时成立.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 打球年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 投中球数y/个 | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2≥2015 | B. | ?x∈R,x2<2015 | C. | ?x∈R,x2≥2015 | D. | ?x∈R,x2>2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
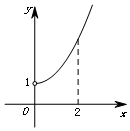 已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数f(x)的单调性相同的是( )
已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数f(x)的单调性相同的是( )| A. | y=x2+1 | B. | y=log2|x| | ||
| C. | y=$\left\{\begin{array}{l}{{e}^{x}(x≥0)}\\{{e}^{-x}(x<0)}\end{array}\right.$ | D. | y=|x+2| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com