
【题目】将正方形![]() 沿对角线
沿对角线![]() 折成直二面角
折成直二面角![]() ,有如下四个结论:
,有如下四个结论:
①![]() ;
;
②![]() 是等边三角形;
是等边三角形;
③![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;
;
④![]() 与
与![]() 所成的角为
所成的角为![]() .
.
其中错误的结论是____________.
【答案】③
【解析】
作出此直二面角的图象,由图形中所给的线面位置关系对四个命题逐一判断,即可得出正确结论.
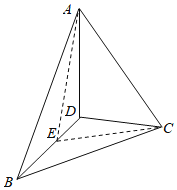
作出如图的图象,其中A﹣BD﹣C=90°,E是BD的中点,可以证明出∠AED=90°即为此直二面角的平面角
对于命题①,由于BD⊥面AEC,故AC⊥BD,此命题正确;
对于命题②,在等腰直角三角形AEC中可以解出AC等于正方形的边长,故△ACD是等边三角形,此命题正确;
对于命题③AB与平面BCD所成的线面角的平面角是∠ABE=45°,故AB与平面BCD成60°的角不正确;
对于命题④可取AD中点F,AC的中点H,连接EF,EH,FH,由于EF,FH是中位线,可证得其长度为正方形边长的一半,而EH是直角三角形的中线,其长度是AC的一半即正方形边长的一半,故△EFH是等边三角形,由此即可证得AB与CD所成的角为60°;
综上知①②④是正确的
故答案为:③


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】公元2222年,有一种高危传染病在全球范围内蔓延,被感染者的潜伏期可以长达10年,期间会有约0.05%的概率传染给他人,一旦发病三天内即死亡,某城市总人口约200万人,专家分析其中约有1000名传染者,为了防止疾病继续扩散,疾病预防控制中心现决定对全市人口进行血液检测以筛选出被感染者,由于检测试剂十分昂贵且数量有限,需要将血样混合后一起检测以节约试剂,已知感染者的检测结果为阳性,末被感染者为阴性,另外检测结果为阳性的血样与检测结果为阴性的血样混合后检测结果为阳性,同一检测结果的血样混合后结果不发生改变.
(1)若对全市人口进行平均分组,同一分组的血样将被混合到一起检测,若发现结果为阳性, 则再在该分组内逐个检测排査,设每个组![]() 个人,那么最坏情况下,需要进行多少次检测可以找到所有的被感染者?在当前方案下,若要使检测的次数尽可能少,每个分组的最优人数?
个人,那么最坏情况下,需要进行多少次检测可以找到所有的被感染者?在当前方案下,若要使检测的次数尽可能少,每个分组的最优人数?
(2)在(1)的检测方案中,对于检测结果为阳性的组来取逐一检测排査的方法并不是很好, 或可将这些组的血样再进行一次分组混合血样检测,然后再进行逐一排査,仍然考虑最坏的情况,请问两次要如何分组,使检测总次数尽可能少?
(3)在(2)的检测方案中,进行了两次分组混合血样检测,仍然考虑最坏情况,若再进行若干次分组混合血样检测,是否会使检测次数更少?请给出最优的检测方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有限集合![]() ,定义如下操作过程
,定义如下操作过程![]() :从
:从![]() 中任取两个元素
中任取两个元素![]() 、
、![]() ,由
,由![]() 中除了
中除了![]() 、以外的元素构成的集合记为
、以外的元素构成的集合记为![]() ;①若
;①若 ,则令
,则令 ;②若
;②若 ,则
,则![]() ;这样得到新集合
;这样得到新集合![]() ,例如集合
,例如集合![]() 经过一次操作后得到的集合可能是
经过一次操作后得到的集合可能是![]() 也可能得到
也可能得到![]() 等,可继续对取定的
等,可继续对取定的![]() 实施操作过程
实施操作过程![]() ,得到的新集合记作
,得到的新集合记作![]() ,……,如此经过
,……,如此经过![]() 次操作后得到的新集合记作
次操作后得到的新集合记作![]() ,设
,设![]() ,对于
,对于![]() ,反复进行上述操作过程,当所得集合
,反复进行上述操作过程,当所得集合![]() 只有一个元素时,则所有可能的集合
只有一个元素时,则所有可能的集合![]() 为______.
为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“石头、剪刀、布”,又称“猜丁壳”,是一种流行多年的猜拳游戏,起源于中国,然后传到日本、朝鲜等地,随着亚欧贸易的不断发展,它传到了欧洲,到了近代逐渐风靡世界.其游戏规则是:出拳之前双方齐喊口令,然后在语音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”、“剪刀”胜“布”、而“布”又胜过“石头”.若所出的拳相同,则为和局.小军和大明两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛,则小军和大明比赛至第四局小军胜出的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
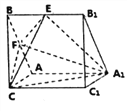
【题目】已知正三棱柱![]() 中,
中, ![]() 分别为
分别为![]() 的中点,设
的中点,设![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角为
的平面角为![]() ,求实数
,求实数![]() 的值,并判断此时二面角
的值,并判断此时二面角![]() 是否为直二面角,请说明理由.
是否为直二面角,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本题共3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知数列![]() 满足
满足![]() .
.
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 是公比为
是公比为![]() 等比数列,
等比数列,![]() ,
,![]() 求
求![]() 的取值范围;
的取值范围;
(3)若![]() 成等差数列,且
成等差数列,且![]() ,求正整数
,求正整数![]() 的最大值,以及
的最大值,以及![]() 取最大值时相应数列
取最大值时相应数列![]() 的公差.
的公差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com