
【题目】函数y=sin2x的图象经过适当变换可以得到y=cos2x的图象,则这种变换可以是( )
A.沿x轴向右平移 ![]() 个单位
个单位
B.沿x轴向左平移 ![]() 个单位
个单位
C.沿x轴向左平移 ![]() 个单位
个单位
D.沿x轴向右平移 ![]() 个单位
个单位
 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2+ax+1(a∈R). (Ⅰ)当a=
x2+ax+1(a∈R). (Ⅰ)当a= ![]() 时,求不等式f(x)<3的解集;
时,求不等式f(x)<3的解集;
(Ⅱ)当0<x<2时,不等式f(x)>0恒成立,求实数a的取值范围;
(Ⅲ)求关于x的不等式f(x)﹣ ![]() a2﹣1>0的解集.
a2﹣1>0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生数学竞赛成绩的频率分布直方图如图所示,成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则该次数学成绩在[50,60)内的人数为( ) 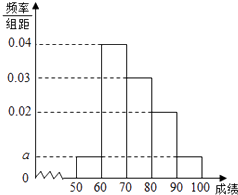
A.20
B.15
C.10
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+1)x+b.
(1)若f(x)<0的解集为(﹣1,3),求a,b的值;
(2)当a=1时,若对任意x∈R,f(x)≥0恒成立,求实数b的取值范围;
(3)当b=a时,解关于x的不等式f(x)<0(结果用a表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,C> ![]() ,若函数y=f(x)在[0,1]上为单调递减函数,则下列命题正确的是( )
,若函数y=f(x)在[0,1]上为单调递减函数,则下列命题正确的是( )
A.f(cosA)>f(cosB)
B.f(sinA)>f(sinB)
C.f(sinA)>f(cosB)
D.f(sinA)<f(cosB)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
.
(Ⅰ)求证:AB⊥PC;
(Ⅱ)求点D到平面PAC的距离.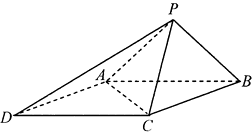
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以下关于向量的命题中,不正确的是( )
A.若向量 ![]() ,向量
,向量 ![]() (xy≠0),则
(xy≠0),则 ![]()
B.若四边形ABCD为菱形,则 ![]()
C.点G是△ABC的重心,则 ![]()
D.△ABC中, ![]() 和
和 ![]() 的夹角等于A
的夹角等于A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中, ![]() 平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形,
平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形, ![]() .
. 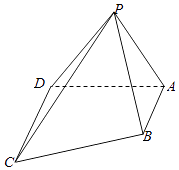
(1)证明:平面PAB⊥平面PCD;
(2)若三棱锥B﹣PAD的体积为 ![]() ,求平面PAD与平面PBC所成二面角的余弦值.
,求平面PAD与平面PBC所成二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com