
已知常数a>0,向量c=(0,a),i=(1,0),经过原点O以c+λi为方向向量的直线与经过定点A(0,a),以i-2λc为方向向量的直线相交于点P.其中λ∈R.试问:是否存在两个定点E、F,使得|PF|+|PF|为定值.若存在,求出E,F的坐标;若不存在,说明理由.
|
解:根据题设条件,首先求出点 P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.∵ i=(1,0),c=(0,a),∴ c+λi=(λ,a),i-2λc=(1,-2λa).因此,直线 OP和AP的方程分别为λy=ax和y-a=-2λax.消去参数λ,得点 P(x,y)的坐标满足方程y(y-a)=-2a2x2,整理得 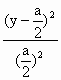 =1 ① =1 ①
因为 a>0,所以得:(i)当a= (ii)当0<a< (iii)当a> |


科目:高中数学 来源: 题型:
| c |
| i |
| c |
| i |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| n |
| m |
| ||
| 2 |
| EM |
| EN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| n |
| m |
查看答案和解析>>
科目:高中数学 来源:2003年江苏省高考数学试卷(解析版) 题型:解答题
 =(0,a),
=(0,a), =(1,0),经过原点O以
=(1,0),经过原点O以 +λ
+λ ,为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.
,为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:2003年天津市高考数学试卷(理科)(解析版) 题型:解答题
 =(0,a),
=(0,a), =(1,0),经过原点O以
=(1,0),经过原点O以 +λ
+λ ,为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.
,为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com