
【题目】在平面直角坐标系 ![]() 中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线
中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线 ![]() 的极坐标方程是
的极坐标方程是 ![]() ,圆
,圆 ![]() 的极坐标方程是
的极坐标方程是 ![]() .
.
(1)求 ![]() 与
与 ![]() 交点的极坐标;
交点的极坐标;
(2)设 ![]() 为
为 ![]() 的圆心,
的圆心, ![]() 为
为 ![]() 与
与 ![]() 交点连线的中点,已知直线
交点连线的中点,已知直线 ![]() 的参数方程是
的参数方程是 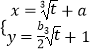 (
( ![]() 为参数),求
为参数),求 ![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】某纺织厂订购一批棉花,其各种长度的纤维所占的比例如下表所示:

(1)请估计这批棉花纤维的平均长度与方差.
(2)如果规定这批棉花纤维的平均长度为4.90厘米,方差不超过1.200,两者允许误差均不超过0.10视为合格产品.请你估计这批棉花的质量是否合格?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 与四棱锥
与四棱锥![]() 的组合体中,已知
的组合体中,已知![]() 平面
平面![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,设
,设![]() 是线段
是线段![]() 中点.
中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且 ![]()

(1)求证:不论 ![]() 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,汉诺塔问题是指有3根杆子A,B,C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面.把B杆上的4个碟子全部移到A杆上,最少需要移动( )次. ( )



A.12 B.15 C.17 D.19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数f(x)中,满足“x1x2∈(0,+∞)且x1≠x2有(x1﹣x2)[f(x1)﹣f(x2)]<0”的是( )
A.f(x)= ![]() ﹣x
﹣x
B.f(x)=x3
C.f(x)=lnx+ex
D.f(x)=﹣x2+2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com