
【题目】某企业生产一种产品,从流水线上随机抽取100件产品,统计其质量指标值并绘制频率分布直方图(如图):
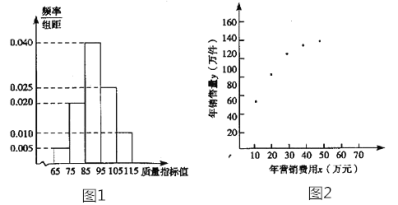
规定产品的质量指标值在![]() 的为劣质品,在
的为劣质品,在![]() 的为优等品,在
的为优等品,在![]() 的为特优品,销售时劣质品每件亏损1元,优等品每件盈利3元,特优品每件盈利5元.以这100 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
的为特优品,销售时劣质品每件亏损1元,优等品每件盈利3元,特优品每件盈利5元.以这100 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该企业为了解年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对近5年年营销费用
(单位:万件)的影响,对近5年年营销费用![]() 和年销售量
和年销售量![]() 数据做了初步处理,得到如图的散点图及一些统计量的值.
数据做了初步处理,得到如图的散点图及一些统计量的值.
|
|
|
|
16.30 | 23.20 | 0.81 | 1.62 |
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
①求![]() 关于
关于![]() 的回归方程;
的回归方程;
⑦用所求的回归方程估计该企业应投人多少年营销费,才能使得该企业的年收益的预报值达到最大?(收益=销售利润营销费用,取![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() 其回归直线
其回归直线![]() 均斜率和截距的最小二乘估计分别为
均斜率和截距的最小二乘估计分别为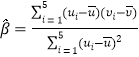 ,
,![]() .
.
【答案】(1)3;(2)①![]() ,②900万元.
,②900万元.
【解析】
(1)先设每件产品的销售利润为![]() ,判断出
,判断出![]() 的可能取值,根据频率分布直方图求出对应概率,进而得出分布列,求出期望;
的可能取值,根据频率分布直方图求出对应概率,进而得出分布列,求出期望;
(2)①先由![]() 得,
得,![]() ,令
,令![]() ,
,![]() ,
,![]() ,则
,则![]() ,根据表中数据求出
,根据表中数据求出![]() ,
,![]() ,进而可得
,进而可得![]() ,从而可得
,从而可得![]() ,整理即可求出结果;
,整理即可求出结果;
②设年收益为![]() 万元,则
万元,则![]() ,令
,令![]() ,则
,则![]() ,进而可求出结果.
,进而可求出结果.
(1)设每件产品的销售利润为![]() ,则
,则![]() 的可能取值为-1,3,5由频率分布直方图可得产品为劣质品、优等品、特优品的概率分别为0.05,0.85,0.1.所以
的可能取值为-1,3,5由频率分布直方图可得产品为劣质品、优等品、特优品的概率分别为0.05,0.85,0.1.所以![]() ;
;![]() ;
;![]() ,…
,…
所以![]() 的分布列为
的分布列为
| -1 | 3 | 5 |
| 0.05 | 0.85 | 0.1 |
所以![]() (元).
(元).
即每件产品的平均销售利润为3元.
(2)①由![]() 得,
得,![]() .
.
令![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
由表中数据可得,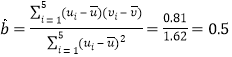 ,
,
则![]() .
.
所以![]() ,即
,即![]() .
.
因为![]() ,所以
,所以![]() ,故所求的回归方程为
,故所求的回归方程为![]() .
.
②设年收益为![]() 万元,则
万元,则![]() .
.
令![]() ,则
,则![]() ,
,
所以当![]() ,即
,即![]() 时,
时,![]() 有最大值900.
有最大值900.
即该企业应该投入900万元营销费,能使得该企业的年收益的预报值达到最大900万元.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各![]() 名,将男性、女性使用微信的时间分成
名,将男性、女性使用微信的时间分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.

(1)根据女性频率分布直方图,估计女性使用微信的平均时间;
(2)若每天玩微信超过![]() 小时的用户列为“微信控”,否则称其为“非微信控”,请你根据已知条件完成
小时的用户列为“微信控”,否则称其为“非微信控”,请你根据已知条件完成![]() 的列联表,并判断是否有
的列联表,并判断是否有![]() 的把握认为“微信控”与“性别”有关?
的把握认为“微信控”与“性别”有关?
参考公式:![]() ,其中
,其中![]() .
.
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值,并求取得最大值时直线
的面积之差的绝对值的最大值,并求取得最大值时直线![]() 的方程.
的方程.![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .已知
.已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程及离心率![]() 的值;
的值;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数![]() .在平面直角坐标系xOy中,已知点
.在平面直角坐标系xOy中,已知点![]() ,直线l:
,直线l:![]() ,曲线Γ:
,曲线Γ:![]() (
(![]() ,
,![]() ).l与x轴交于点A、与Γ交于点B.P、Q分别是曲线Γ与线段AB上的动点.
).l与x轴交于点A、与Γ交于点B.P、Q分别是曲线Γ与线段AB上的动点.
(1)用t表示点B到点F的距离;
(2)设![]() ,
,![]() ,线段OQ的中点在直线FP上,求△AQP的面积;
,线段OQ的中点在直线FP上,求△AQP的面积;
(3)设![]() ,是否存在以FP、FQ为邻边的矩形FPEQ,使得点E在Γ上?若存在,求点P的坐标;若不存在,说明理由.
,是否存在以FP、FQ为邻边的矩形FPEQ,使得点E在Γ上?若存在,求点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与直线
与直线![]() 交于
交于![]() 两点,点
两点,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() 离心率
离心率![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)经过椭圆左焦点![]() 的直线(不经过点
的直线(不经过点![]() 且不与
且不与![]() 轴重合)与椭圆交于
轴重合)与椭圆交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .则是否存在常数
.则是否存在常数![]() ,使得向量
,使得向量![]()
![]() 共线?若存在求出
共线?若存在求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面ABCD是边长为3的正方形,EFG分别是棱ABPBPC的中点,
,底面ABCD是边长为3的正方形,EFG分别是棱ABPBPC的中点,![]() ,
,![]() .
.

(Ⅰ)求证:平面EFG∥平面PAD;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() 垂直
垂直![]() 交
交![]() 于
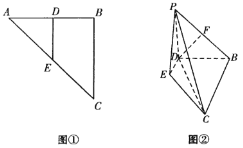
于![]() ,如图①.将
,如图①.将![]() 沿
沿![]() 折起,使
折起,使![]() 到达
到达![]() 的位置,且使平面
的位置,且使平面![]() 平面
平面![]() ,连接
,连接![]() ,
,![]() ,如图②.
,如图②.
(Ⅰ)若![]() 为
为![]() 的中点,
的中点,![]() ,求证:
,求证:![]() ;
;
(Ⅱ)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com