圆x2+y2=1与x,y轴的正半轴分别相交于A,B两点.
(Ⅰ)求AB所在的直线方程;
(Ⅱ)过点A做两条互相垂直的直线分别与圆交于P,Q两点,试求△PAQ面积的最大值,并指出此时PQ所在的直线方程.
解:(I)由题可知A(1,0),B(0,1)…(1分),所以AB所在的直线方程y=-x+1…(3分)
(II)解法1:由题可知直线AP,AQ的斜率都存在,且不能为0,…(4分)
设AP的斜率为k,则AQ的斜率为
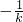
,AP的直线方程为kx-y-k=0
所以

,从而:

…(6分)
同理得:

,所以

…(8分)
(当且仅当k=±1时等号成立)
所以△PAQ面积的最大值为1,此时PQ的方程为x=0…(10分)
解法2:由题可知∠PAQ始终为直角,所以PQ必通过圆心,从而|PQ|=2
当A点距离PQ最远时,即△PAQ为等腰直角三角形时,
△PAQ面积取最大值1
此时PQ的方程为x=0
分析:(I)由已知圆x
2+y
2=1与x,y轴的正半轴分别相交于A,B两点,我们易求出A,B两个点的坐标,代入两点式方程,整理后即可得到AB所在的直线方程;
(Ⅱ)解法一:由题可知直线AP,AQ的斜率都存在,且不能为0,分别设AP的斜率为k,则AQ的斜率为
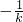
,则我们易求出AP及AQ的长(含参数k),代入三角形面积公式,利用基本不等式式,即可得到答案.
解法二:若∠PAQ始终为直角,则PQ必为圆的直径,当A点距离PQ最远时,即△PAQ为等腰直角三角形时,△PAQ面积最大.
点评:本题考查的知识点是直线和圆的方程的应用,直线的一般式方程,(1)的关键是求出A,B两点的坐标,(2)的关键关键法一是写出△PAQ面积的表达式,法二是得到PQ是圆的直径.

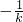 ,AP的直线方程为kx-y-k=0
,AP的直线方程为kx-y-k=0 ,从而:
,从而: …(6分)
…(6分) ,所以
,所以 …(8分)
…(8分)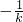 ,则我们易求出AP及AQ的长(含参数k),代入三角形面积公式,利用基本不等式式,即可得到答案.
,则我们易求出AP及AQ的长(含参数k),代入三角形面积公式,利用基本不等式式,即可得到答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案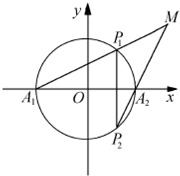 如图,A1、A2为圆x2+y2=1与x轴的两个交点,P1P2为垂直于x轴的弦,且A1P1与A2P2的交点为M.
如图,A1、A2为圆x2+y2=1与x轴的两个交点,P1P2为垂直于x轴的弦,且A1P1与A2P2的交点为M.