
【题目】在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF. 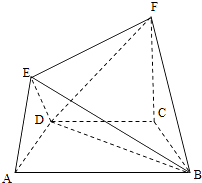
(1)求证:BD⊥平面AED;
(2)求二面角F﹣BD﹣C的余弦值.
【答案】
(1)证明:因为四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°.所以∠ADC=∠BCD=120°.又CB=CD,
所以∠CDB=30°,因此,∠ADB=90°,AD⊥BD,
又AE⊥BD且,AE∩AD=A,AE,AD平面AED,
所以BD⊥平面AED;
(2)解法一:由(1)知,AD⊥BD,同理AC⊥BC,
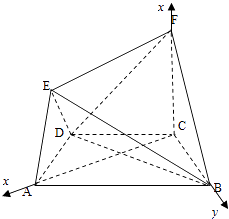
又FC⊥平面ABCD,因此CA,CB,CF两两垂直,以C为坐标原点,分别以CA,CB,CF所在的直线为X轴,Y轴,Z轴建立如图的空间直角坐标系,
不妨设CB=1,则C(0,0,0),B(0,1,0),D( ![]() ,﹣
,﹣ ![]() ,0),F(0,0,1),因此
,0),F(0,0,1),因此 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,0),
,0), ![]() =(0,﹣1,1)
=(0,﹣1,1)
设平面BDF的一个法向量为 ![]() =(x,y,z),则
=(x,y,z),则 ![]()
![]() =0,
=0, ![]()
![]() =0
=0
所以x= ![]() y=
y= ![]() z,取z=1,则
z,取z=1,则 ![]() =(
=( ![]() ,1,1),
,1,1),
由于 ![]() =(0,0,1)是平面BDC的一个法向量,
=(0,0,1)是平面BDC的一个法向量,
则cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() ,所以二面角F﹣BD﹣C的余弦值为
,所以二面角F﹣BD﹣C的余弦值为 ![]()
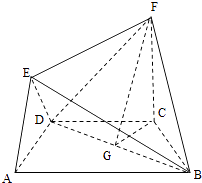
解法二:取BD的中点G,连接CG,FG,由于 CB=CD,因此CG⊥BD,又FC⊥平面ABCD,BD平面ABCD,
所以FC⊥BD,由于FC∩CG=C,FC,CG平面FCG.
所以BD⊥平面FCG.故BD⊥FG,所以∠FGC为二面角F﹣BD﹣C的平面角,
在等腰三角形BCD中,由于∠BCD=120°,
因此CG= ![]() CB,又CB=CF,
CB,又CB=CF,
所以GF= ![]() =
= ![]() CG,
CG,
故cos∠FGC= ![]() ,
,
所以二面角F﹣BD﹣C的余弦值为 ![]()
【解析】(1)由题意及图可得,先由条件证得AD⊥BD及AE⊥BD,再由线面垂直的判定定理即可证得线面垂直;(2)解法一:由(1)知,AD⊥BD,可得出AC⊥BC,结合FC⊥平面ABCD,知CA,CA,CF两两垂直,因此可以C为坐标原点,分别以CA,CB,CF所在的直线为X轴,Y轴,Z轴建立如图的空间直角坐标系,设CB=1,表示出各点的坐标,再求出两个平面的法向量的坐标,由公式求出二面角F﹣BD﹣C的余弦值即可;
解法二:取BD的中点G,连接CG,FG,由于 CB=CD,因此CG⊥BD,又FC⊥平面ABCD,BD平面ABCD,可证明出∠FGC为二面角F﹣BD﹣C的平面角,再解三角形求出二面角F﹣BD﹣C的余弦值.
【考点精析】掌握直线与平面垂直的判定和向量语言表述线面的垂直、平行关系是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可;设直线![]() 的方向向量是
的方向向量是![]() ,平面
,平面![]() 内的两个相交向量分别为
内的两个相交向量分别为![]() ,若
,若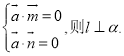 .
.


科目:高中数学 来源: 题型:
【题目】设10≤x1<x2<x3<x4≤104 , x5=105 , 随机变量ξ1取值x1、x2、x3、x4、x5的概率均为0.2,随机变量ξ2取值 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 的概率也均为0.2,若记Dξ1、Dξ2分别为ξ1、ξ2的方差,则( )
的概率也均为0.2,若记Dξ1、Dξ2分别为ξ1、ξ2的方差,则( )
A.Dξ1>Dξ2
B.Dξ1=Dξ2
C.Dξ1<Dξ2
D.Dξ1与Dξ2的大小关系与x1、x2、x3、x4的取值有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)设![]() ,若函数
,若函数![]() 的图象的一条对称轴为直线
的图象的一条对称轴为直线![]() ,求
,求![]() 的值;
的值;
(2)若将![]() 的图象向左平移
的图象向左平移![]() 个单位,或者向右平移
个单位,或者向右平移![]() 个单位得到的图象都过坐标原点,求所有满足条件的
个单位得到的图象都过坐标原点,求所有满足条件的![]() 和
和![]() 的值;
的值;
(3)设![]() ,
,![]() ,已知函数
,已知函数![]() 在区间
在区间![]() 上的所有零点依次为
上的所有零点依次为![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
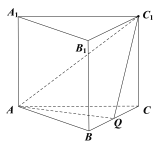
【题目】如图,在正三棱柱(底面为正三角形的直棱柱)ABC-A1B1C1中,已知AB=AA1=2,点Q为BC的中点.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面AQC1的距离.
到平面AQC1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
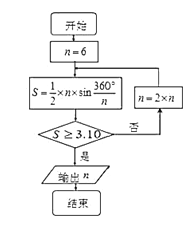
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出![]() 的值为 ( )
的值为 ( )
(参考数据:![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,雾霾日趋严重,雾霾的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题,某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律,每生产该型号空气净化器![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入
(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)求利润函数![]() 的解析式(利润=销售收入-总成本);
的解析式(利润=销售收入-总成本);
(2)工厂生产多少百台产品时,可使利润最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com