在某个QQ群中有n名同学在玩一种叫“数字哈哈镜”的游戏.这些同学编号依次为1,2,3,….,n..在哈哈镜中,每个同学看到的像用数对(p,q)表示.规则如下:编号为k的同学看到的像为(ak,ak+1),且满足ak+1-ak=k(k∈N*),已知编号为1的同学看到的像为(5,6),则编号为4的同学看到的像为 ;某位同学看到的像为(195,q),其中q的值被遮住了,请你帮这位同学猜出q= .
【答案】
分析:由游戏规则中“编号为k的同学看到像为(p,q)中的(a
k,a
k+1),编号为k+1的同学看到像为(a
k+1,a
k+2),这样就找到了游戏进行的一个联系,同时注意到a
k+1-a
k=k(k∈N*),至此,本题中的题意就浮现出来.
解答:解:(1)由题意规律,编号为1的同学看到的像是(5,6),
∴编号为2的同学看到的像是(6,8),
编号为3的同学看到的像是(8,11),
编号为4的同学看到的像是(11,15).
(2)设编号为n的同学看到的像是(b
n,a
n),
则b
1=5,a
1=6,当n≥2时,b
n=a
n-1.
由题意a
n-b
n=n,∴a
n-a
n-1=n(n≥2).
∴a
n-a
1=(a
2-a
1)+(a
3-a
2)+…+(a
n-a
n-1)
=2+3+…n=
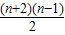
..
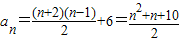
,
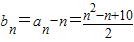
,
当

=195时,n=20,
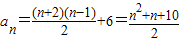
=
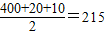
.
故答案为:(11,15),215.
点评:本题以QQ作为背景、以数字哈哈镜面游戏规则形式给出信息,考查学生阅读信息、搜集信息、加工信息的能力.考查灵活运用数列知识分析问题与解决问题的能力.

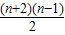 ..
..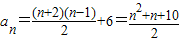 ,
,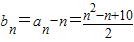 ,
, =195时,n=20,
=195时,n=20,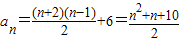 =
=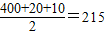 .
.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案