
【题目】某工厂生产某种电子产品,每件产品合格的概率均为![]() ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验
,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验![]() 件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每
件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每![]() 个(
个(![]() )一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或
)一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或![]() 次.设该工厂生产
次.设该工厂生产![]() 件该产品,记每件产品的平均检验次数为
件该产品,记每件产品的平均检验次数为![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)试说明,当![]() 越大时,该方案越合理,即所需平均检验次数越少;
越大时,该方案越合理,即所需平均检验次数越少;
(ii)当![]() 时,求使该方案最合理时
时,求使该方案最合理时![]() 的值及
的值及![]() 件该产品的平均检验次数.
件该产品的平均检验次数.
【答案】(1)分布列详见解析,期望![]() ;(2)(i)详见解析;(ii)
;(2)(i)详见解析;(ii)![]() 时平均检验次数最少,约
时平均检验次数最少,约![]() 次.
次.
【解析】
(1)根据每![]() 个(
个(![]() )一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或
)一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或![]() 次,每件产品的平均检验次数
次,每件产品的平均检验次数![]() 的可能取值为
的可能取值为![]() ,
,![]() ,再利用独立事件和互斥事件求得概率列出分布列,再求期望
,再利用独立事件和互斥事件求得概率列出分布列,再求期望
(2)(i)由(1)知![]() ,根据指数函数的单调性得到
,根据指数函数的单调性得到![]() 在
在![]() 上单调递减,从而得到结论. (ii)由(1)记
上单调递减,从而得到结论. (ii)由(1)记![]() ,则由
,则由![]() 且取最小值时,该方案最合理求解.
且取最小值时,该方案最合理求解.
(1)由题意,![]() 的可能取值为
的可能取值为![]() ,
,![]()
![]() ,
,![]() ,
,
故![]() 的分布列为
的分布列为
|
|
|
|
|
|
![]()
(2)(i)由(1),记![]() ,
,
因为![]() .所以
.所以![]() 在
在![]() 上单调递减,
上单调递减,
故![]() 越大,
越大,![]() 越小,即所需平均检验次数越少,该方案越合理.
越小,即所需平均检验次数越少,该方案越合理.
(ii)记![]() ,当
,当![]() 且取最小值时,该方案最合理,
且取最小值时,该方案最合理,
因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() 时平均检验次数最少,约
时平均检验次数最少,约![]() 次.
次.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
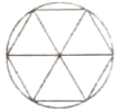
【题目】刘徽(约公元225年—295年),魏晋期间伟大的数学家,中国古典数学理论的奠基人之一.他在割圆术中提出的“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”.这可视为中国古代极限观念的佳作.割圆术的核心思想是将一个圆的内接正![]() 边形等分成
边形等分成![]() 个等腰三角形(如图所示),当
个等腰三角形(如图所示),当![]() 变得很大时,这
变得很大时,这![]() 个等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,估计
个等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,估计![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (t为参数),
(t为参数),![]() ,点A为直线
,点A为直线![]() 与曲线C在第二象限的交点,过O点的直线
与曲线C在第二象限的交点,过O点的直线![]() 与直线
与直线![]() 互相垂直,点B为直线
互相垂直,点B为直线![]() 与曲线C在第三象限的交点.
与曲线C在第三象限的交点.
(1)写出曲线C的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在郊野公园的景观河的两岸,![]() 、
、![]() 是夹角为120°的两条岸边步道(长度均超过
是夹角为120°的两条岸边步道(长度均超过![]() 千米),为方便市民观光游览,现准备在河道拐角处的另一侧建造一个观景台
千米),为方便市民观光游览,现准备在河道拐角处的另一侧建造一个观景台![]() ,在两条步道
,在两条步道![]() 、
、![]() 上分别设立游客上下点
上分别设立游客上下点![]() 、
、![]() ,从
,从![]() 、
、![]() 到观景台
到观景台![]() 建造两条游船观光线路
建造两条游船观光线路![]() 、
、![]() ,测得
,测得![]() 千米.
千米.
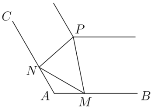
(1)求游客上下点![]() 、
、![]() 间的距离;
间的距离;
(2)若![]() ,设
,设![]() ,求两条观光线路
,求两条观光线路![]() 与
与![]() 之和关于
之和关于![]() 的表达式
的表达式![]() ,并求其最大值.
,并求其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生产线的技术改造前后各20次连续正常运行的时间长度(单位:天)数据,并绘制了如茎叶图:
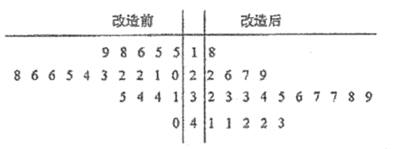
(1)(i)设所采集的40个连续正常运行时间的中位数m,并将连续正常运行时间超过m和不超过m的次数填入下面的列联表:
超过 | 不超过 | |
改造前 | ||
改造后 |
(ii)根据(i)中的列联表,能否有99%的把握认为生产线技术改造前后的连续正常运行时间有差异?
附: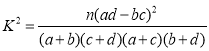
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)工厂的生产线的运行需要进行维护,工厂对生产线的生产维护费用包括正常维护费、保障维护费两种.对生产线设定维护周期为T天(即从开工运行到第kT天![]() 进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元/次;保障维护费第一次为0.2万元/周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:
进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元/次;保障维护费第一次为0.2万元/周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:![]() ,
,![]() .以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列.
.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
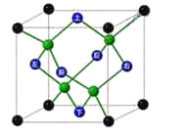
【题目】金刚石是碳原子的一种结构晶体,属于面心立方晶胞(晶胞是构成晶体的最基本的几何单元),即碳原子处在立方体的![]() 个顶点,
个顶点,![]() 个面的中心,此外在立方体的对角线的
个面的中心,此外在立方体的对角线的![]() 处也有
处也有![]() 个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有
个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有![]() 个按照正四面体分布的碳原子.设金刚石晶胞的棱长为
个按照正四面体分布的碳原子.设金刚石晶胞的棱长为![]() ,则正四面体
,则正四面体![]() 的棱长为__________;正四面体
的棱长为__________;正四面体![]() 的外接球的体积是__________.
的外接球的体积是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com