
【题目】设椭圆![]() :
: ![]() 的左、右焦点
的左、右焦点![]() 、
、![]() ,其焦距为
,其焦距为![]() ,点
,点![]() 在椭圆的内部,点
在椭圆的内部,点![]() 是椭圆
是椭圆![]() 上的动点,且
上的动点,且![]() 恒成立,则椭圆离心率的取值范围是__________.
恒成立,则椭圆离心率的取值范围是__________.
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c.满足2acosC+bcosC+ccosB=0.
(Ⅰ)求角C的大小;
(Ⅱ)若a=2,△ABC的面积为![]() ,求C的大小。
,求C的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 平面内一个三角形各边所在的直线都与另一个平面平行,则这两个平面平行;
B. 若两个平面平行,则分别位于这两个平面的直线也互相平行;
C. 平行于同一个平面的两个平面平行;
D. 若两个平面平行,则其中一个平面内的直线平行于另一个平面;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数①![]() ,②
,②![]() ,③
,③![]() ,
,
判断如下两个命题的真假:
命题甲: ![]() 在区间
在区间![]() 上是增函数;
上是增函数;
命题乙: ![]() 在区间
在区间![]() 上恰有两个零点
上恰有两个零点![]() ,且
,且![]() .
.
能使命题甲、乙均为真的函数的序号是
A. ① B. ② C. ①③ D. ①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:![]() 的焦点为F,
的焦点为F,![]() 是抛物线E上一点,且
是抛物线E上一点,且![]() .
.
![]() 1
1![]() 求抛物线E的标准方程;
求抛物线E的标准方程;
![]() 2
2![]() 设点B是抛物线E上异于点A的任意一点,直线AB与直线
设点B是抛物线E上异于点A的任意一点,直线AB与直线![]() 交于点P,过点P作x轴的垂线交抛物线E于点M,设直线BM的方程为
交于点P,过点P作x轴的垂线交抛物线E于点M,设直线BM的方程为![]() ,k,b均为实数,请用k的代数式表示b,并说明直线BM过定点.
,k,b均为实数,请用k的代数式表示b,并说明直线BM过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园里有一湖泊,其边界由两条线段![]() 和以
和以![]() 为直径的半圆弧
为直径的半圆弧![]() 组成,其中
组成,其中![]() 为2百米,
为2百米,![]() 为
为![]() .若在半圆弧
.若在半圆弧![]() ,线段
,线段![]() ,线段
,线段![]() 上各建一个观赏亭
上各建一个观赏亭![]() ,再修两条栈道
,再修两条栈道![]() ,使
,使![]() . 记
. 记![]() .
.

(1)试用![]() 表示
表示![]() 的长;
的长;
(2)试确定点![]() 的位置,使两条栈道长度之和最大.
的位置,使两条栈道长度之和最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 图象向左平移
图象向左平移![]() 个单位,再把各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再把各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,则下列说法中正确的是( )
的图象,则下列说法中正确的是( )
A.![]() 的最大值为
的最大值为![]() B.
B.![]() 是奇函数
是奇函数
C.![]() 的图象关于点
的图象关于点![]() 对称D.
对称D.![]() 在
在![]() 上单调递减
上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
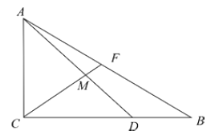
【题目】在三角形ABC中,![]() ,
,![]() ,
,![]() ,D是线段BC上一点,且
,D是线段BC上一点,且![]() ,F为线段AB上一点.
,F为线段AB上一点.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的取值范围;
的取值范围;
(3)若![]() 为线段
为线段![]() 的中点,直线
的中点,直线![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com