练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设A>0,求函数f(x)=－1n(x+A)(x∈（0，+∞）)的单调区间.

    答案：
    解析：

    		f＇（x）=－(x>0).

    当A>0,x>0时，

    f＇（x）>0x2+(2A－4)x+A2>0,

    f＇（x）<0 x2+(2A－4)x+A2<0.

    ①当A>1时，对所有x>0,有x2+(2A－4)x+A2>0，

    即f＇（x）>0.

    此时f＇（x）在（0,+∞）内单调递增.

    ②当A=1时，对x≠1，有x2+(2A－4)x+A2>0，

    即f＇（x）>0此时f＇（x）在（0,1）内单调递增，在（1,+∞）内单调递增.

    又知函数f(x)在x=1处连续.

    因此，函数f(x)在（0,+∞）内单调递增.

    ③当0<A>1时，令f＇（x）>0,即x2+(2A－4)x+A2>0,解得，x<2－A－2,或x>2－A+2.

    因此，函数f(x)在区间（0,2－A－2）内单调递增，在区间（2－A+2,+∞）内也单调递增.

    令f＇（x）<0,即x2+(2A－4)x+A2<0，解得2－A－2<x<2－A+2.

    因此，函数f(x)在区间（2－A－2，2－A+2.）内单调递减.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    设A>0,求函数f(x)=－1n(x+A)(x∈（0，+∞）)的单调区间.

    查看答案和解析>>

    科目：高中数学 来源：2014届安徽省宿州市高二第二次月考数学试卷（解析版） 题型：解答题

    设函数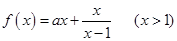

    （1）若a>0,求函数的最小值；

    （2）若a是从1，2，3三个数中任取一个数，b是从2，3，4，5四个数中任取一个数，求f (x)>b恒成立的概率。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设a＞0,求函数f(x)=-ln(x+a)(x＞0)的单调区间.

    查看答案和解析>>

    科目：高中数学 来源：河南省新乡市2010届高三二模（理） 题型：解答题

     

    设a>0，函数f(x)=x2+a|lnx－1|.

    （Ⅰ）当a=1时，求曲线y=f(x)在x=1出的切线方程；

    （II）当x∈[1，+∞)时，求函数f(x)的最小值.

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案