
分析 (1)求出${f}^{'}(x)=a+\frac{1}{x}$,由导当我性质得f(x)的增区间为(0,-$\frac{1}{a}$),减区间为(-$\frac{1}{a}$,e).从而f(x)max=f(-$\frac{1}{a}$)=-1-1+ln(-$\frac{1}{a}$)=-3,由此能求出a.
(2)函数g(x)=|f(x)|-$\frac{lnx}{x}$-$\frac{b}{2}$存在零点,即方程|f(x)|=$\frac{lnx}{x}$+$\frac{b}{2}$有实数根,令h(x)=$\frac{lnx}{x}$+$\frac{b}{2}$,则h′(x)=$\frac{1-lnx}{{x}^{2}}$,由此利用导数性质能求出实数b的取值范围.
解答 (本题满分12分)
解:(1)∵函数f(x)=ax+lnx-1,其中a为常数,
∴${f}^{'}(x)=a+\frac{1}{x}$,
令f′(x)=0,得x=-$\frac{1}{a}$,
∵a∈(-∞,-$\frac{1}{e}$),∴0<-$\frac{1}{a}$<e,
由f′(x)>0,解得0<x<-$\frac{1}{a}$,
由f′(x)<0,得-$\frac{1}{a}<x<e$,
∴f(x)的增区间为(0,-$\frac{1}{a}$),减区间为(-$\frac{1}{a}$,e).
∴f(x)max=f(-$\frac{1}{a}$)=-1-1+ln(-$\frac{1}{a}$)=-3,
解得a=-e.
(2)函数g(x)=|f(x)|-$\frac{lnx}{x}$-$\frac{b}{2}$存在零点,
即方程|f(x)|=$\frac{lnx}{x}$+$\frac{b}{2}$有实数根,
由已知函数f(x)的定义域为{x|x>0},
当a=-$\frac{1}{e}$时,f(x)=-$\frac{x}{e}$-1+lnx,
当0<x<e时,f′(x)>0;当x>e时,f′(x)<0.
∴f(x)的增区间为(0,e),减区间为(e,+∞),
∴f(x)max=f(e)=-1,∴|f(x)|≥1,
令h(x)=$\frac{lnx}{x}$+$\frac{b}{2}$,则h′(x)=$\frac{1-lnx}{{x}^{2}}$,
当0<x<e时,h′(x)>0,
当x>e时,h′(x)<0,
从而函数h(x)在(0,e)上单调递增,在(e,+∞)上单调递减,
∴h(x)max=h(e)=$\frac{1}{e}+\frac{b}{2}$,
要使方程|f(x)|=$\frac{lnx}{x}+\frac{b}{2}$有实数根,
只需h(x)min=h(e)=$\frac{1}{e}+\frac{b}{2}≥1$即可,∴b≥2-$\frac{2}{e}$,
∴实数b的取值范围是[2-$\frac{2}{e}$,+∞).
点评 本题考查实数值及实数的取值范围的求法,是中档题,解题时要认真审题,注意导数性质、构造法的合理运用.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
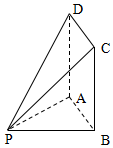 如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
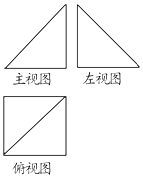 如图,已知某几何体的主视图和左视图是全等的等腰直角三角形,俯视图是边长为2的正方形,那么它的体积是( )
如图,已知某几何体的主视图和左视图是全等的等腰直角三角形,俯视图是边长为2的正方形,那么它的体积是( )| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1或1 | C. | 2 | D. | -2或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{π}{8}+\frac{1}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{4}+\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$]∪[2,+∞) | B. | [$\frac{1}{2}$,2] | C. | (-∞,-2]∪[-$\frac{1}{2}$,+∞) | D. | [-$\frac{1}{2}$,-2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com