
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.(
的取值范围.(![]() 是自然对数的底数,
是自然对数的底数,![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)代入a值,求函数的导数,由导数的几何意义求得切线斜率,根据点斜式可得切线方程;(2)求导数,通过讨论a的范围,求函数单调区间,结合函数单调性和函数的最值可求a的范围;(3)求g(x)解析式,求函数导数,讨论函数单调性,由函数单调性和最值可确定a的范围.
(1)当![]() 时,
时,![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以切线方程为![]() .
.
(2)![]() ,
,
①当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 单调递增,
单调递增,
因为![]() ,所以
,所以![]() 有唯一零点,即
有唯一零点,即![]() 符合题意;
符合题意;
②当![]() 时,令
时,令![]() ,解得
,解得![]() ,列表如下:
,列表如下:
|
|
|
|
| - | 0 | + |
|
| 极小值 |
|
由表可知,![]() .
.
(i)当![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() 符合题意;
符合题意;
(ii)当![]() ,即
,即![]() 时,
时,![]() ,
,
因为![]() ,且
,且![]() ,所以
,所以![]() ,
,
故存在![]() ,使得
,使得![]() ,所以
,所以![]() 不符题意;
不符题意;
(iii)当![]() ,即
,即![]() 时,
时,![]() ,
,
因为![]() ,
,
设![]() ,
,
则![]() ,
,
所以![]() 单调递增,即
单调递增,即![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
故存在![]() ,使得
,使得![]() ,所以
,所以![]() 不符题意;
不符题意;
综上,![]() 的取值范围为
的取值范围为![]() .
.
(3)![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() 符合题意;
符合题意;
②当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 单调递增,
单调递增,
又因为
![]() ,
,
所以存在![]() ,使得
,使得![]() ,
,
且当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() 不符题意;
不符题意;
综上,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,它的一个顶点A与抛物线
,它的一个顶点A与抛物线![]() 的焦点重合.
的焦点重合.
![]() 1
1![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 2
2![]() 是否存在直线l,使得直线l与椭圆C交于M,N两点,且椭圆C的右焦点F恰为
是否存在直线l,使得直线l与椭圆C交于M,N两点,且椭圆C的右焦点F恰为![]() 的垂心
的垂心![]() 三条高所在直线的交点
三条高所在直线的交点![]() ?若存在,求出直线l的方程:若不存在,说明理由.
?若存在,求出直线l的方程:若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园要设计如图所示的景观窗格(其结构可以看成矩形在四个角处对称地截去四个全等的三角形所得,如图二中所示多边形![]() ),整体设计方案要求:内部井字形的两根水平横轴
),整体设计方案要求:内部井字形的两根水平横轴![]() 米,两根竖轴
米,两根竖轴![]() 米,记景观窗格的外框(如图二实线部分,轴和边框的粗细忽略不计)总长度为
米,记景观窗格的外框(如图二实线部分,轴和边框的粗细忽略不计)总长度为![]() 米.
米.

(1)若![]() ,且两根横轴之间的距离为
,且两根横轴之间的距离为![]() 米,求景观窗格的外框总长度;
米,求景观窗格的外框总长度;
(2)由于预算经费限制,景观窗格的外框总长度不超过![]() 米,当景观窗格的面积(多边形
米,当景观窗格的面积(多边形![]() 的面积)最大时,给出此景观窗格的设计方案中
的面积)最大时,给出此景观窗格的设计方案中![]() 的大小与
的大小与![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某品牌饮料的某种食品添加剂是否超标,现对该品牌下的两种饮料一种是碳酸饮料![]() 含二氧化碳
含二氧化碳![]() ,另一种是果汁饮料
,另一种是果汁饮料![]() 不含二氧化碳
不含二氧化碳![]() 进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶
进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶![]() 均是
均是![]() 组成的一个样本,进行了检测,得到了如下茎叶图
组成的一个样本,进行了检测,得到了如下茎叶图![]() 根据国家食品安全规定当该种添加剂的指标大于
根据国家食品安全规定当该种添加剂的指标大于![]() 毫克
毫克![]() 为偏高,反之即为正常.
为偏高,反之即为正常.
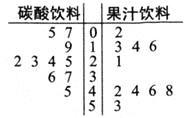
(1)依据上述样本数据,完成下列![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
正常 | 偏高 | 合计 | |
碳酸饮料 | |||
果汁饮料 | |||
合计 |
(2)现从食品添加剂偏高的样本中随机抽取2瓶饮料去做其它检测,求这两种饮料都被抽到的概率.
参考公式: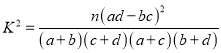 ,其中
,其中![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,圆C的参数方程为![]() 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
![]() 1
1![]() 求圆C的普通方程和直线l的直角坐标方程;
求圆C的普通方程和直线l的直角坐标方程;
![]() 2
2![]() 设M是直线l上任意一点,过M做圆C切线,切点为A、B,求四边形AMBC面积的最小值.
设M是直线l上任意一点,过M做圆C切线,切点为A、B,求四边形AMBC面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 平面
平面![]() ,且四边形
,且四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() .
.

(1)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(2)点![]() 是线段
是线段![]() 上的动点,当直线
上的动点,当直线![]() 与
与![]() 所成的角最小时,求线段
所成的角最小时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生将语文、数学、英语、物理、化学、生物6科的作业安排在周六、周日完成,要求每天至少完成两科,且数学,物理作业不在同一天完成,则完成作业的不同顺序种数为( )
A. 600B. 812C. 1200D. 1632
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com