【答案】
分析:设二次函数f(x)=ax
2+bx+c(a≠0)
(I)由图象知函数的图象过(0,),(8,0),最大值为16,代入可求a,b,c,从而可求函数f(x)的解析式
(Ⅱ)由f(x)=-(x-4)
2+16,要求函数f(x)在区间[t,t+2]上的最大值h(t),需要考查对称轴x=4与区间[t,t+4]的位置关系:分t>4,t≤4≤t+2,t+2<4分别求解函数的最大值
(Ⅲ)构造函数φ(x)=g(x)-f(x)=x
2-8x+6lnx+m.要使函数f(x)与函数g(x)有且仅有2个不同的交点,则函数φ(x)=x
2-8x+6lnx+m的图象与x轴的正半轴有且只有两个不同的交点,结合导数的知识可得必须且只须
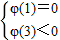
或
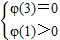
,从而可求m的范围
解答:解:设二次函数f(x)=ax
2+bx+c(a≠0)
(I)由图象知:

,
∴函数f(x)的解析式为f(x)=-x
2+8x…(4分)
(Ⅱ)∵f(x)=-(x-4)
2+16,
∴当t>4时,f(x)的最大值是f(t)=-(t-4)
2+16;
当t≤4≤t+2,即2≤t≤4时,f(t)的最大值是f(4)=16;
当t+2<4,即t<2时,f(x)的最大值是f(t+2)=-(t-2)
2+16.∴
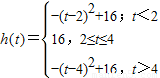
…(8分)
(Ⅲ)令φ(x)=g(x)-f(x),则g(x)-f(x)=x
2-8x+6lnx+m.
因为x>0,要使函数f(x)与函数g(x)有且仅有2个不同的交点,则函数φ(x)=x
2-8x+6lnx+m的图象与x轴的正半轴有且只有两个不同的交点
∴
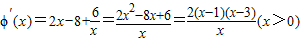
当x∈(0,1)时,φ′(x)>0,φ(x)是增函数;
当x∈(1,3)时,φ′(x)<0,φ(x)是减函数
当x∈(3,+∞)时,φ′(x)>0,φ(x)是增函数
当x=1或x=3时,φ′(x)=0
∴φ(x)极大值为φ(1)=m-7;φ(x)极小值为φ(3)=m+6ln3-15…(12分)
又因为当x→0时,φ(x)→-∞
当x→+∞时,φ(x)→+∞
所以要使φ(x)=0有且仅有两个不同的正根,只须
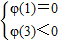
或
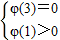
即
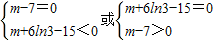
∴m=7或m=15-6ln3.
∴当m=7或m=15-6ln3.时,函数f(x)与g(x)的图象有且只有两个不同交点.…(14分)
点评:本题目考查了由二次函数的图象求解函数的解析式,考查了识别图象的能力及二次函数性质的应用,函数与方程的相互转化的思想在解题中的应用.

 已知二次函数y=f(x)的图象如图所示.
已知二次函数y=f(x)的图象如图所示.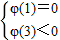 或
或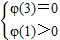 ,从而可求m的范围
,从而可求m的范围 ,
,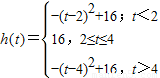 …(8分)
…(8分)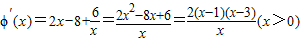
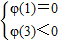 或
或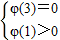
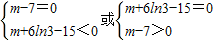


 已知二次函数y=f(x)的图象如图所示:
已知二次函数y=f(x)的图象如图所示: