
【题目】已知椭圆E的方程为![]() (
(![]() ),
),![]() ,
,![]() 分别为椭圆的左右焦点,A,B为椭圆E上关于原点对称两点,点M为椭圆E上异于A,B一点,直线
分别为椭圆的左右焦点,A,B为椭圆E上关于原点对称两点,点M为椭圆E上异于A,B一点,直线![]() 和直线
和直线![]() 的斜率
的斜率![]() 和
和![]() 满足:
满足:![]() .
.
(1)求椭圆E的标准方程;
(2)过![]() 作直线l交椭圆于C,D两点,且
作直线l交椭圆于C,D两点,且![]() (
(![]() ),求
),求![]() 面积的取值范围.
面积的取值范围.
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】低碳经济时代,文化和旅游两大产业逐渐成为我国优先发展的“绿色朝阳产业”.为了解某市的旅游业发展情况,某研究机构对该市2019年游客的消费情况进行随机调查,得到频数分布表及频率分布直方图.
旅游消费(千元) |
|
|
|
|
频数(人) | 10 | 60 |
|
|
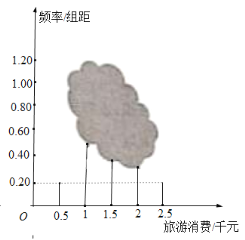
(1)由图表中数据,求![]() 的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
(2)该机构利用最小二乘法得到2013~2017年该市的年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归模型:
的线性回归模型:![]() .
.
注:年份代码1~5分别对应年份2013~2017
①试求2013~2017年的年旅游人次的平均值;
②据统计,2018年该市的年旅游人次为9千万人次.建立2013~2018年该市年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归方程,并估计2019年该市的年旅游收入.
的线性回归方程,并估计2019年该市的年旅游收入.
注:年旅游收入=年旅游人次×人均消费
参考数据:![]() .参考公式:
.参考公式: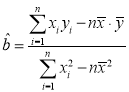 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)直线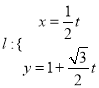 (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数).在以
为参数).在以![]() 为极点、
为极点、![]() 轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线
轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线![]() :
:![]() 的焦点
的焦点![]() 的极坐标为
的极坐标为![]() .
.
(1)求常数![]() 的值;
的值;
(2)设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)将曲线![]() 上所有点的横坐标不变,纵坐标缩短到原来的
上所有点的横坐标不变,纵坐标缩短到原来的![]() 倍,得到曲线
倍,得到曲线![]() ,若
,若![]() 与
与![]() 的交点为
的交点为![]() (异于坐标原点
(异于坐标原点![]() ),
),![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为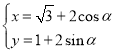 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() ,(t为参数),在以原点为极点,x轴正半轴为极轴的极坐标中,曲线
,(t为参数),在以原点为极点,x轴正半轴为极轴的极坐标中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将![]() 与
与![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若曲线![]() 与
与![]() 的公共点都在
的公共点都在![]() 上,
上,![]() ,求r.
,求r.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)过点(1,
(a>b>0)过点(1,![]() ),过椭圆C的一个焦点作与长轴垂直的直线,被椭圆C截得的弦长为1
),过椭圆C的一个焦点作与长轴垂直的直线,被椭圆C截得的弦长为1
(1)求椭圆C的标准方程
(2)已知点P为椭圆C上不同于顶点的一点,A,B为椭圆C的左,右顶点,直线AP,BP分别与直线x=﹣6交于M,N两点设线段MN中点为Q,求![]() 的取最小值时点Q的坐标.
的取最小值时点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com