
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)求证:点![]() 在直线
在直线![]() 上;
上;
(3)是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(1)![]() (2)详见解析(3)存在,且
(2)详见解析(3)存在,且![]()
【解析】
(1)根据离心率和焦点坐标列方程组,解方程组求得![]() 的值,进而求得椭圆
的值,进而求得椭圆![]() 的方程.(2)写出直线
的方程.(2)写出直线![]() 的方程,联立直线的方程和椭圆的方程,求得中点
的方程,联立直线的方程和椭圆的方程,求得中点![]() 的坐标,将坐标代入直线
的坐标,将坐标代入直线![]() 的方程,满足方程,由此证得点
的方程,满足方程,由此证得点![]() 在直线
在直线![]() 上.(3)由(2)知
上.(3)由(2)知![]() 到
到![]() 的距离相等,根据两个三角形面积的关系,得到
的距离相等,根据两个三角形面积的关系,得到![]() 是
是![]() 的中点,设出
的中点,设出![]() 点的坐标,联立直线
点的坐标,联立直线![]() 的方程和椭圆的方程,求得
的方程和椭圆的方程,求得![]() 点的坐标,并由此求得
点的坐标,并由此求得![]() 的值.
的值.
解:(1) 解:由 ,解得
,解得![]() ,
,![]()
所以所求椭圆的标准方程为![]()
(2)设![]() ,
,![]() ,
,![]() ,
,
![]() ,消
,消![]() 得,
得,![]() ,
,
解得
将![]() 代入到
代入到![]() 中,满足方程
中,满足方程
所以点![]() 在直线
在直线![]() 上.
上.
(3)由(2)知![]() 到
到![]() 的距离相等,
的距离相等,
若![]() 的面积是
的面积是![]() 面积的3倍,得
面积的3倍,得![]() ,
,
有![]() ,
,
∴![]() 是
是![]() 的中点,
的中点,
设![]() ,则
,则![]() ,
,
联立![]() ,解得
,解得![]() ,
,
于是![]()
解得![]() ,所以
,所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某市一次全市高中男生身高统计调查数据显示:全市![]() 名男生的身高服从正态分布
名男生的身高服从正态分布![]() .现从某学校高三年级男生中随机抽取
.现从某学校高三年级男生中随机抽取![]() 名测量身高,测量发现被测学生身高全部介于
名测量身高,测量发现被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分组:
之间,将测量结果按如下方式分组: ![]() ,
, ![]() ,…,
,…, ![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这![]() 名男生身高在
名男生身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(Ⅲ)在这![]() 名男生身高在
名男生身高在![]() 以上(含
以上(含![]() )的人中任意抽取
)的人中任意抽取![]() 人,该
人,该![]() 人中身高排名(从高到低)在全市前
人中身高排名(从高到低)在全市前![]() 名的人数记力
名的人数记力![]() ,求
,求![]() 的数学期望.
的数学期望.
参考数据:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 的定义域为
的定义域为![]() ,且满足如下两个条件:①
,且满足如下两个条件:①![]() 在
在![]() 内是单调递增函数;②存在
内是单调递增函数;②存在![]() ,使得
,使得![]() 在
在![]() 上的值域为
上的值域为![]() ,那么就称函数
,那么就称函数![]() 为“希望函数”,若函数
为“希望函数”,若函数![]() 是“希望函数”,求实数
是“希望函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.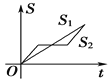 B.
B.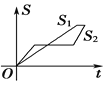 C.
C.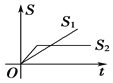 D.
D.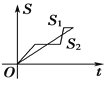
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司决定对旗下的某商品进行一次评估,该商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住2022年冬奥会契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和销售策略改革,并提高定价到![]() 元.公司拟投入
元.公司拟投入![]() 万作为技改费用,投入50万元作为固定宣传费用,投入
万作为技改费用,投入50万元作为固定宣传费用,投入![]() 万元作为浮动宣传费用.试问:当该商品改革后的销售量
万元作为浮动宣传费用.试问:当该商品改革后的销售量![]() 至少达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() 函数
函数![]() 在
在![]() 上单调递减;命题
上单调递减;命题![]() 曲线
曲线![]() 为双曲线.
为双曲线.
(Ⅰ)若“![]() 且
且![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com