
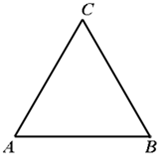
 如图,△ABC为一个等腰三角形形状的空地,腰CA的长为3(百米),底AB的长为4(百米).现决定在空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.
如图,△ABC为一个等腰三角形形状的空地,腰CA的长为3(百米),底AB的长为4(百米).现决定在空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.| S1 | S2 |
| 3 |
| 2 |
| 1 |
| 2 |
| AC2+AB2-BC2 |
| 2AC×AB |
| 2 |
| 3 |
| 15 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
| 5 |
| S1 |
| S2 |
2
| ||||
|
| 48 |
| 25 |
| x+y |
| 2 |
| 25 |
| 4 |
| 5 |
| 2 |
| S1 |
| S2 |
| 23 |
| 25 |
| 5 |
| 2 |
| 23 |
| 25 |
| c |
| sinC |
| a |
| sinA |
4
| ||
| 9 |
| S1 |
| S2 |
| 11 |
| 25 |
| 5 |
| 2 |
| 11 |
| 25 |


科目:高中数学 来源: 题型:
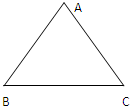 (2011•江西模拟)如图,△ABC为一个等腰三角形的空地,底边AB长为4(百米),腰长为3(百米),现决定在空地上修一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形周长相等,面积分别为S1和S2,
(2011•江西模拟)如图,△ABC为一个等腰三角形的空地,底边AB长为4(百米),腰长为3(百米),现决定在空地上修一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形周长相等,面积分别为S1和S2,| S1 | S2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三下学期开学质量检测数学试卷 题型:解答题
(本小题满分14分)如图,△ABC为一个等腰三角形形状的空地,腰CA的长为3(百米),底AB的长为4(百米).现决定在该空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.
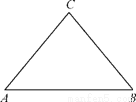
(1) 若小路一端E为AC的中点,求此时小路的长度;
(2) 求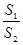 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011年广东省深圳市高级中学高考数学模拟试卷(理科)(解析版) 题型:解答题
 的最小值.
的最小值.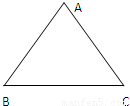
查看答案和解析>>
科目:高中数学 来源:2011年江苏省苏、锡、常、镇四市高三调研数学试卷(一)(解析版) 题型:解答题
 的最小值.
的最小值.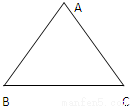
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com