(x+1)
2+(y+3)
2=9或(x-1)
2+(y-3)
2=9
分析:设出圆的标准方程,表示出圆心坐标和半径r,由圆心在直线3x-y=0上,把圆心坐标代入方程得到关于a与b的关系式,用a表示出b,又根据圆与x轴相切,得到圆心的纵坐标的绝对值等于半径r,用a表示出半径r,将表示出的b及r代入圆的方程,利用点到直线的距离公式表示出圆心到直线x-y=0的距离d,根据垂径定理得到弦的一半,圆的半径r及弦心距构成直角三角形,根据勾股定理列出关于a的方程,求出方程的解得到a的值,代入即可确定出圆的方程.
解答:设圆的方程为:(x-a)
2+(y-b)
2=r
2,
所以圆心坐标为(a,b),半径为r(r>0),
由圆心在3x-y=0上,得到3a-b=0,即b=3a;
又圆与x轴相切,得到r=|b|=|3a|,
则圆的方程变形为:(x-a)
2+(y-3a)
2=9a
2,
所以圆心到直线x-y=0的距离d=

,
根据垂径定理及勾股定理得:

+

=9a
2,
化简得:a
2=1,解得a=±1,
则所求圆的方程为:(x+1)
2+(y+3)
2=9或(x-1)
2+(y-3)
2=9.
故答案为:(x+1)
2+(y+3)
2=9或(x-1)
2+(y-3)
2=9
点评:此题考查了直线与圆相交的性质,点到直线的距离公式,垂径定理及勾股定理.要求学生会利用待定系数法求圆的方程,根据垂径定理垂直于弦则平分弦,由弦的一半,圆的半径及弦心距构成的直角三角形,利用勾股定理解决问题.

 ,则这个圆的标准方程为:________.
,则这个圆的标准方程为:________. ,
, +
+ =9a2,
=9a2,

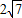 ,则这个圆的标准方程为: .
,则这个圆的标准方程为: .