
【题目】若实数x,y满足x2-4xy+4y2+4x2y2=4,则当x+2y取得最大值时,![]() 的值为________.
的值为________.
【答案】2
【解析】
(解法1)因为实数x,y满足x2-4xy+4y2+4x2y2=4,所以(x+2y)2+4x2y2-8xy=4,即(x+2y)2+4(xy-1)2=8,所以(x+2y)2=8-4(xy-1)2,所以当(xy-1)2=0时,即xy=1时,x+2y取得最大值,此时x=![]() ,y=
,y=![]() ,所以
,所以![]() =2.(解法2)因为实数x,y满足x2-4xy+4y2+4x2y2=4,所以(x-2y)2+4x2y2=4,令x-2y=2cosθ,xy=sinθ,则(x+2y)2=(x-2y)2+8xy=4cos2θ+8sinθ,所以(x+2y)2=-4sin2θ+8sinθ+4,所以当sinθ=1时,(x+2y)2取得最大值,此时xy=1,x-2y=0,所以
=2.(解法2)因为实数x,y满足x2-4xy+4y2+4x2y2=4,所以(x-2y)2+4x2y2=4,令x-2y=2cosθ,xy=sinθ,则(x+2y)2=(x-2y)2+8xy=4cos2θ+8sinθ,所以(x+2y)2=-4sin2θ+8sinθ+4,所以当sinθ=1时,(x+2y)2取得最大值,此时xy=1,x-2y=0,所以![]() =2.
=2.


科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在x轴上的椭圆,离心率![]() ,且经过抛物线
,且经过抛物线![]() 的焦点.若过点
的焦点.若过点![]() 的直线
的直线![]() 斜率不等于零
斜率不等于零![]() 与椭圆交于不同的两点E、
与椭圆交于不同的两点E、![]() 在B、F之间
在B、F之间![]() ,
,
![]() 求椭圆的标准方程;
求椭圆的标准方程;
![]() 求直线l斜率的取值范围;
求直线l斜率的取值范围;
![]() 若
若![]() 与
与![]() 面积之比为
面积之比为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】英国统计学家E.H.辛普森1951年提出了著名的辛普森悖论,下面这个案例可以让我们感受到这个悖论.有甲乙两名法官,他们都在民事庭和行政庭主持审理案件,他们审理的部分案件被提出上诉.记录这些被上述案件的终审结果如下表所示(单位:件):
法官甲 | 法官乙 | ||||||
终审结果 | 民事庭 | 行政庭 | 合计 | 终审结果 | 民事庭 | 行政庭 | 合计 |
维持 | 29 | 100 | 129 | 维持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合计 | 32 | 118 | 150 | 合计 | 100 | 25 | 125 |
记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为
,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,则下面说法正确的是
,则下面说法正确的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,焦点为
上,焦点为![]() ,圆O的直径为
,圆O的直径为![]() .
.

(1)求椭圆C及圆O的标准方程;
(2)设直线l与圆O相切于第一象限内的点P,且直线l与椭圆C交于![]() 两点.记
两点.记![]() 的面积为
的面积为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() .
.
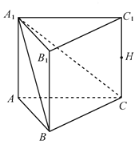
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国已进入新时代中国特色社会主义时期,人民生活水平不断提高.某市随机统计了城区若干户市民十月人均生活支出比九月人均生活支出增加量(记为P元)的情况,并根据统计数据制成如图频率分布直方图.
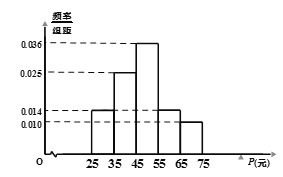
(1)根据频率分布直方图估算P的平均值![]() ;
;
(2)若该市城区有4户市民十月人均生活支出比九月人均生活支出分别增加了42元,50元,52元,60元,从这4户中随机抽取2户,求这2户P值的和超过100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如下图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(1)不改变车票价格,减少支出费用;建议(2)不改变支出费用,提高车票价格.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
的函数关系如下图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(1)不改变车票价格,减少支出费用;建议(2)不改变支出费用,提高车票价格.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )

A.①反映建议(2),③反映建议(1)B.①反映建议(1),③反映建议(2)
C.②反映建议(1),④反映建议(2)D.④反映建议(1),②反映建议(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() 且满足
且满足![]() ,
,![]() (
(![]() 为常数,
为常数,![]() ).
).
(1)求![]() ;
;
(2)若数列![]() 是等比数列,求实数
是等比数列,求实数![]() 的值;
的值;
(3)是否存在实数![]() ,使得数列
,使得数列![]() 满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的值;若不存在,请说明理由.
满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为信号源点,
为信号源点,![]() 、
、![]() 、
、![]() 是三个居民区,已知
是三个居民区,已知![]() 、
、![]() 都在
都在![]() 的正东方向上,
的正东方向上,![]() ,
,![]() ,
,![]() 在
在![]() 的北偏西45°方向上,
的北偏西45°方向上,![]() ,现要经过点
,现要经过点![]() 铺设一条总光缆直线
铺设一条总光缆直线![]() (
(![]() 在直线
在直线![]() 的上方),并从
的上方),并从![]() 、
、![]() 、
、![]() 分别铺设三条最短分支光缆连接到总光缆
分别铺设三条最短分支光缆连接到总光缆![]() ,假设铺设每条分支光缆的费用与其长度的平方成正比,比例系数为1元/
,假设铺设每条分支光缆的费用与其长度的平方成正比,比例系数为1元/![]() ,设
,设![]() ,(
,(![]() ),铺设三条分支光缆的总费用为
),铺设三条分支光缆的总费用为![]() (元).
(元).
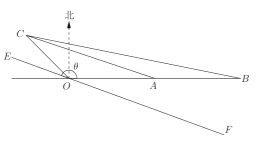
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)求![]() 的最小值及此时
的最小值及此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com