
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的首项
的首项![]() 及数列的递推关系式
及数列的递推关系式![]() ;
;
(2)若数列![]() 成等比数列,求常数
成等比数列,求常数![]() 的值,并求数列
的值,并求数列![]() 的通项公式;
的通项公式;
(3)数列![]() 中是否存在三项
中是否存在三项![]() 、
、![]() 、
、![]() ,它们组成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
,它们组成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,(
,(![]() 为正整数)都在函数
为正整数)都在函数![]() 的图象上.
的图象上.
(1)若数列![]() 是等差数列,证明:数列
是等差数列,证明:数列![]() 是等比数列;
是等比数列;
(2)设![]() ,过点
,过点![]() 的直线与两坐标轴所围成的三角形面积为
的直线与两坐标轴所围成的三角形面积为![]() ,试求最小的实数
,试求最小的实数![]() ,使
,使![]() 对一切正整数
对一切正整数![]() 恒成立;
恒成立;
(3)对(2)中的数列![]() ,对每个正整数
,对每个正整数![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个3,得到一个新的数列
个3,得到一个新的数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试探究2016是否是数列
项和,试探究2016是否是数列![]() 中的某一项,写出你探究得到的结论并给出证明.
中的某一项,写出你探究得到的结论并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李克强总理在很多重大场合都提出“大众创业,万众创新”.某创客,白手起家,2015年一月初向银行贷款十万元做创业资金,每月获得的利润是该月初投入资金的![]() .每月月底需要交纳房租和所得税共为该月全部金额(包括本金和利润)的
.每月月底需要交纳房租和所得税共为该月全部金额(包括本金和利润)的![]() ,每月的生活费等开支为3000元,余款全部投入创业再经营.如此每月循环继续.
,每月的生活费等开支为3000元,余款全部投入创业再经营.如此每月循环继续.
(1)问到2015年年底(按照12个月计算),该创客有余款多少元?(结果保留至整数元)
(2)如果银行贷款的年利率为![]() ,问该创客一年(12个月)能否还清银行贷款?
,问该创客一年(12个月)能否还清银行贷款?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某商场2018年洗衣机、电视机和电冰箱三种电器各季度销量的百分比堆积图(例如:第3季度内,洗衣机销量约占![]() ,电视机销量约占
,电视机销量约占![]() ,电冰箱销量约占
,电冰箱销量约占![]() ).根据该图,以下结论中一定正确的是( )
).根据该图,以下结论中一定正确的是( )
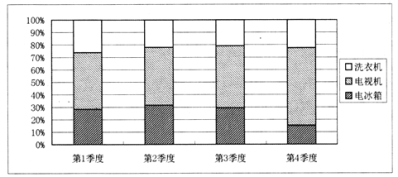
A. 电视机销量最大的是第4季度
B. 电冰箱销量最小的是第4季度
C. 电视机的全年销量最大
D. 电冰箱的全年销量最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() (
(![]() )交于
)交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点,
为坐标原点,![]() .
.
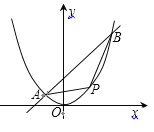
(1)求直线![]() 的方程和抛物线
的方程和抛物线![]() 的方程;
的方程;
(2)若抛物线![]() 上一动点
上一动点![]() 从
从![]() 到
到![]() 运动时(
运动时(![]() 不与
不与![]() 、
、![]() 重合),求
重合),求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照如下规则构造数表:第一行是:2;第二行是:![]() ;即3,5,第三行是:
;即3,5,第三行是:![]() 即4,6,6,8;
即4,6,6,8;![]() (即从第二行起将上一行的数的每一项各项加1写出,再各项加3写出)
(即从第二行起将上一行的数的每一项各项加1写出,再各项加3写出)
2
3,5
4,6,6,8
5,7,7,9,7,9,9,11
……………………………………
若第![]() 行所有的项的和为
行所有的项的和为![]() .
.
(1)求![]() ;
;
(2)试求![]() 与
与![]() 的递推关系,并据此求出数列
的递推关系,并据此求出数列![]() 的通项公式;
的通项公式;
(3)设![]() ,求
,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的动点.
上的动点.
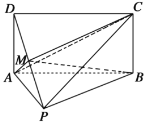
(1)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积记为
的体积记为![]() ,四棱锥
,四棱锥![]() 的体积记为
的体积记为![]() ,当
,当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com