
分析 根据题意求出f(x)的解析式,再判断出函数的单调性,即可得到答案.
解答 解:由a⊙b=$\left\{\begin{array}{l}{b,a≥b}\\{a,a<b}\end{array}\right.$,
得,f(x)=x?(2-x)=$\left\{\begin{array}{l}{2-x,x≥1}\\{x,x<1}\end{array}\right.$,
∴f(x)在(-∞,1)上是增函数,在[1,+∞)上是减函数,
∴f(x)≤1,
故答案为:1.
点评 本题考查分段函数的值域,即每段值域的并集,也是一个新定义运算问题:取两者中较小的一个,求出函数的解析式并判断出其单调性是解题的关键.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
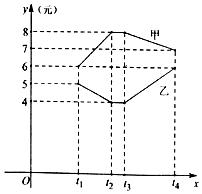 甲乙两种商品在过去一段时间内的价格走势如图所示,假设某人持有资金120万元,他可以在t1至t4的任意时刻买卖这两种商品,且买卖能够立即成交(其他费用忽略不计),那么他持有的资金最多可变为( )
甲乙两种商品在过去一段时间内的价格走势如图所示,假设某人持有资金120万元,他可以在t1至t4的任意时刻买卖这两种商品,且买卖能够立即成交(其他费用忽略不计),那么他持有的资金最多可变为( )| A. | 120万元 | B. | 160万元 | C. | 220万元 | D. | 240万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k1<k2<k3 | B. | k2<k1<k3 | C. | k3<k2<k1 | D. | k1<k3<k2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2015}{2016}$ | B. | $\frac{2015}{1008}$ | C. | $\frac{2015}{672}$ | D. | $\frac{2015}{336}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com