
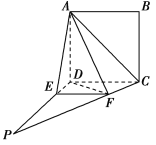
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
(1)证明:CF⊥平面ADF;
(2)求二面角DAFE的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)结合已知又直线和平面垂直的判定定理可判![]() F,即得所求;
F,即得所求;
(2)由已知数据求出必要的线段的长度,建立空间直角坐标系,由向量法计算即可.
(1)证明:∵PD⊥平面ABCD,AD平面ABCD,
∴PD⊥AD.
又CD⊥AD,PD∩CD=D,∴AD⊥平面PCD.
又PC平面PCD,∴AD⊥PC.
又AF⊥PC,AD∩AF=A,∴PC⊥平面ADF,即CF⊥平面ADF.
(2)设AB=1,则在Rt△PCD中,CD=1,
 又∠DPC=30°,∴PC=2,PD=
又∠DPC=30°,∴PC=2,PD=![]() ,∠PCD=60°.
,∠PCD=60°.
由(1)知CF⊥DF,∴DF=CDsin 60°=![]() ,CF=CDcos 60°=
,CF=CDcos 60°=![]() .
.
又FE∥CD,∴![]() =
=![]() =
=![]() ,∴DE=
,∴DE=![]() .
.
同理EF=![]() CD=
CD=![]() .
.
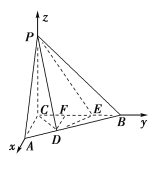
如图所示,以D为原点,建立空间直角坐标系Dxyz,
则A(0,0,1),E![]() ,F
,F![]() ,P(
,P(![]() ,0,0),C(0,1,0).
,0,0),C(0,1,0).
设m=(x,y,z)是平面AEF的一个法向量,则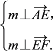
又![]() =
=![]() ,
,![]() =
=![]() ,∴
,∴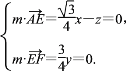
令x=4,则z=![]() ,m=(4,0,
,m=(4,0,![]() ).由(1)知平面ADF的一个法向量为
).由(1)知平面ADF的一个法向量为![]() =(-
=(-![]() ,1,0),
,1,0),
设二面角 DAFE的平面角为θ,可知θ为锐角,
故cos θ=|cos〈m,![]() 〉|=
〉|=![]() =
=![]() =
=![]() .
.
故二面角DAFE的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】给出下列结论:
①“![]() 且
且![]() 为真”是“
为真”是“![]() 或
或![]() 为真”的充分不必要条件:②“
为真”的充分不必要条件:②“![]() 且
且![]() 为假”是“
为假”是“![]() 或
或![]() 为真”的充分不必要条件;③“
为真”的充分不必要条件;③“![]() 或
或![]() 为真”是“非
为真”是“非![]() 为假”的必要不充分条件;④“非
为假”的必要不充分条件;④“非![]() 为真”是“
为真”是“![]() 且
且![]() 为假”的必要不充分条件.
为假”的必要不充分条件.
其中,正确的结论是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸未,甲申、乙酉、丙戌…癸巳,…,共得到60个组合,称六十甲子,周而复始,无穷无尽。2019年是“干支纪年法”中的己亥年,那么2026年是“干支纪年法”中的
A. 甲辰年B. 乙巳年C. 丙午年D. 丁未年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .直线
.直线![]() ,
,![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() .记点
.记点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程.
的方程.
(Ⅱ)已知直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() ,轨迹
,轨迹![]() 在点
在点![]() 处的切线与线段
处的切线与线段![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的底面是正三角形,侧棱长均相等,
的底面是正三角形,侧棱长均相等,![]() 是棱
是棱![]() 上的点(不含端点),记直线
上的点(不含端点),记直线![]() 与直线
与直线![]() 所成角为
所成角为![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com