
 如图,四棱锥P-ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{13}$,M,N分别为BC,PA的中点
如图,四棱锥P-ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{13}$,M,N分别为BC,PA的中点分析 (1)取AD中点E,连接BE,NE,则BE∥MD,NE∥PD,利用面面平行,证明线面平行;
(2)利用面积关系,求平面PAB与平面PCD所成的锐二面角的大小.
解答 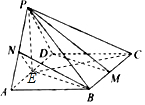 (1)证明:取AD中点E,连接BE,NE,则BE∥MD,NE∥PD,
(1)证明:取AD中点E,连接BE,NE,则BE∥MD,NE∥PD,
∵BE∩NE=E,MD∩PD=D,
∴平面BEN∥平面MDP,
∵BN?平面BEN,
∴BN∥平面PDM
(2)解:连接EP,EC,则PE=3,EB=2$\sqrt{3}$,EC=$\sqrt{16+4-2×4×2×(-\frac{1}{2})}$=2$\sqrt{7}$
∴PB=$\sqrt{21}$,PC=$\sqrt{37}$,
∴cos∠PAB=$\frac{13+16-21}{2\sqrt{13}×4}$=-$\frac{1}{4\sqrt{13}}$,cos∠PDC=$\frac{13+16-37}{2\sqrt{13}×4}$=-$\frac{1}{\sqrt{13}}$,
∴sin∠PAB=$\frac{\sqrt{207}}{4\sqrt{13}}$,sin∠PDC=$\frac{\sqrt{12}}{\sqrt{13}}$,
∴平面PAB与平面PCD所成的锐二面角的余弦值为$\frac{8}{\sqrt{69}}$,大小为arccos$\frac{8\sqrt{69}}{69}$.
点评 本题考查线面平行的判定,考查二面角平面角的计算,考查学生分析解决问题的能力,属于中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
| A. | .. | B. | $\frac{9}{8}$ | C. | $\frac{8}{9}$ | D. | $\frac{25}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
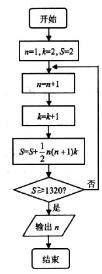 元代数学家朱世杰所著《四元玉鉴》一书,是中国古代数学的重要著作之一,共分卷首、上卷、中卷、下卷四卷,下卷中《果垛叠藏》第一问是:“今有三角垛果子一所,值钱一贯三百二十文,只云从上一个值钱二文,次下层层每个累贯一文,问底子每面几何?”据此,绘制如图所示程序框图,求得底面每边的果子数n为( )
元代数学家朱世杰所著《四元玉鉴》一书,是中国古代数学的重要著作之一,共分卷首、上卷、中卷、下卷四卷,下卷中《果垛叠藏》第一问是:“今有三角垛果子一所,值钱一贯三百二十文,只云从上一个值钱二文,次下层层每个累贯一文,问底子每面几何?”据此,绘制如图所示程序框图,求得底面每边的果子数n为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-y+8=0 | B. | x-3y+8=0 | C. | 3x+y+8=0 | D. | 3x+y+4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a>0,c<0,d>0 | B. | a>0,c>0,d<0 | C. | a<0,c<0,d<0 | D. | a<0,c>0,d<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com